Интересный текст из жж Андрея Фирсова.
Текст Анатолия Сорокина
Краткое содержание предыдущих частей ([1], [2], [3], [4], [5], [6], [7]): в них были рассмотрены необходимые и достаточные условия для успешного использования принятых на вооружение РККА 122-мм пушек А-19 при дальней стрельбе.
И во всех разобранных случаях рефреном проходил один и тот же мотив: при управлении огнём необходимы вычисления, необходимы сложные вычисления, необходимы очень сложные вычисления… С одной стороны, с учётом того, что «всяк кулик своё болото хвалит» (автор этих заметок получил первоначальную подготовку по ВУС артиллерийского вычислителя), может быть это преувеличение и так ли оно важно по сравнению со всем прочим? Подумаешь, складывай, умножай, дели, вычитай. Но на самом деле это равноценный со «стволами» и средствами артиллерийской разведки компонент точной стрельбы. Просто потому что без любой из этих вещей при наличии двух других цель останется так и останется непоражённой. Стрелять при отсутствии правильных преобразований координат цели, координат орудия и всех сопутствующих данных в установки прицела и угломера конечно можно, но вот попаданий здесь точно не будет (случай нализавшейся в зюзю Фортуны, полностью отдавшейся такому управляющему огнём после большого бодуна для обоих, не рассматривается в принципе).
В качестве примера можно привести практические результаты огня для самых-самых суперпушек – морских линкорных. Огонь этих орудий по состоянию на начало 1940-х гг. направлялся по данным с радиолокационных станций и командно-дальномерных пунктов (КДП) с очень совершенным оптическим стадиа- и гониометрическим оборудованием. В установки прицела и целика каждой из башен они пересчитывались на большей частью электромеханических вычислительных устройствах, учитывающих расстояние до цели, скорости как цели, так и корабля-носителя этих пушек, метеоусловия, величину перелёта/недолёта и отклонения по фронту в сухопутной терминологии. Кое-где в таких системах управления огнём уже начинали применяться даже электронные аналоговые схемы, для резервирования имелись методики ручного счёта, таблицы и номограммы. Эффективность при надлежащем функционировании всех этих устройств могла быть потрясающей.
Собственно говоря, гитлеровский линкор «Бисмарк» отправил так на дно Его Величества Корабль (ЕВК) «Худ» и прогнал с нанесением повреждений ещё один ЕВК, «Принц Уэльсский». Однако несколько позже, когда рейдер сам стал объектом охоты и лишился управляемости от авиационной торпеды, добивать его поручили всё-таки британским артиллерийским кораблям. Казалось бы, что он сумеет задорого продать свою жизнь, однако в самом начале артиллерийской дуэли с ЕВК «Родней» «Бисмарк» получил попадание в пост, где находилось управляющее его огнём оборудование, которое оказалось полностью выведенным из строя. При этом были убиты несколько единиц живой силы гитлеровцев, которые занимались его обслуживанием и могли считать огневые данные сами. Тут сильно подфартило уже британцам (но по делу, а не с упоминавшегося выше большого бодуна). Пусть это было не так зрелищно, как попадание в погреб боеприпасов «Худа», но последствия в итоге для «Бисмарка» оказались практически теми же. В результате ещё при исправных пушках и работающем запасном командно-дальномерном пункте точность огня гитлеровского линкора стала нулевой (он так ни разу и не попал в британские корабли, добившись лишь одного близкого разрыва с «Роднеем»). А по нему работали точно и, несмотря на чудеса боевой устойчивости его броневой цитадели против британских снарядов и торпед, «Бисмарк» быстро утратил исправность всех своих пушек, превратившись в итоге в чадящую развалину на волнах. И финал был тот же, что и у «Худа» – упокоение на морском дне. Вот что значит отсутствие точной и своевременной обработки огневых данных.
В отличие от гордых пенителей морей, сухопутные артиллеристы (не зенитчики) не имели «продвинутых» инструментальных систем управления огнём, хотя сложность стрельбы у них была подчас и выше, чем у моряков (те всегда полагались на пристрелку). А как мы видели в предыдущих сериях, на «тверди земной» при выполнении ряда условий можно обойтись и без неё. Конечно, неплохо было бы иметь такое оборудование, но в те годы оно занимало целые отсеки боевого корабля и «кушало» десятки киловатт электрической мощности. Сколько нужно было бы автомашин с его блоками и источниками питания, и какова была бы скорость их свёртывания/развёртывания на нужном месте (плюс проходимость по распутице) – вопрос чисто риторический. Пример 47-го пушечного артиллерийского артполка, вооружённого 122-мм пушками обр. 1931/37 гг., наглядно показывает, что в напряжённой боевой обстановке эта часть металась «туда-сюда» и возить за собой целую колонну вычислительной техники ей было точно не к месту, ибо весь свой автотранспорт чуть ли не целиком задействовался для перевозки боеприпасов, которые расходовались ужасающими темпами. Посему советским артиллеристам приходилось надеяться на свои головы, заранее сделанные таблицы и алгоритмы вычислений. Плюс ещё простейшие средства механизации счёта, которые умещались в сумках, планшетах, портфелях, «сидорах» и т. п. предметах походной экипировки.
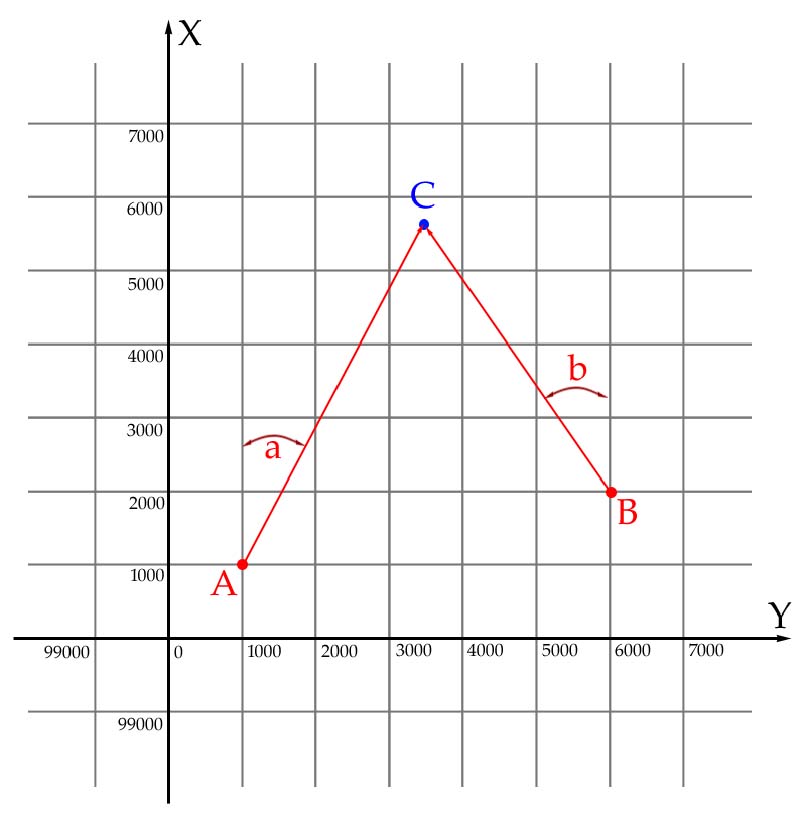
После такого пространнейшего введения мы как раз и рассмотрим, что помогало точно направлять стрельбу наших дальнобойных пушек. Но перед этим, чтобы понять, с чем приходится иметь дело, разберём одну математическую задачу, которая широко используется в артиллерийской практике: а именно нахождение координат точки пересечения двух лучей на плоскости, если для каждого из них известны координаты их начала и углы от заданного направления. Это находит своё применение и для звукометрии, и для расчётов, связанных с сопряжённым наблюдением.
Вспомним школьный курс алгебры касательно уравнения прямой на плоскости:
y = x * tg a + A для прямой, частью которой является первый луч;
y = x * tg b + B для прямой, частью которой является второй луч.
Коэффициенты А и В найдём из знания того факта, что первый луч начинается в точке (Ха, Ya), а второй – в (Xb, Yb):
Ya = Xa * tg a + A, т. е. A = Ya – Xa * tg a, аналогично и B = Yb – Xb * tg b;
Приравниваем оба уравнения прямых друг другу, чтобы найти координату Xc:
Xc * tg a + Ya – Xa * tg a = Xc * tg b + Yb – Xb * tg b;
В итоге получаем:
Хc = (Xa * tg a – Xb * tg b + Yb – Ya) / (tg a – tg b);
Yc = (Xc – Xa)* tg a + Ya.
Стоит упомянуть, что уравнение прямой в «артиллерийской» декартовой системе координат точно также выглядит также, как и в «цивильной», поскольку и там, и там угол отсчитывается от оси X в направлении оси Y, невзирая на разные ориентации оных. Может быть, именно поэтому артиллеристы направили ось Х вверх, в направлении географического севера, от которого отсчитываются дирекционные углы для объектов на местности.
Заметим себе, что знаки у тангенсов могут быть какие угодно и на практике положение точек А и В выбирают таким образом, чтобы минимизировать погрешность алгоритма расчёта, чтобы он не увеличивал сильно погрешности в исходных данных. Увы, без потери точности при счёте не обойтись, но такова уж природа вещей, но об этом чуть ниже. А пока посчитаем число математических операций, нужных для вычисления искомых координат:
- два вычисления тригонометрических функций;
- три умножения;
- шесть сложений и вычитаний (они могут превращаться друг в друга из-за знаков тангенсов углов);
- одно деление.
А теперь откладываем в сторону все имеющиеся средства электронно-вычислительной техники, берём лист бумаги, карандаш (как в годы Великой Отечественной войны), таблицы тригонометрических функций в артиллерийском исчислении (или в гражданском вроде небезызвестного для античных школяров издания Брадиса – автору его ещё удалось застать в самом начале своей одиннадцатиклассной одиссеи – но тогда будем готовы переводить тысячные в радианы ещё дополнительной парой умножений). Каково будет время на то, чтобы высчитать координаты с точностью до единиц метров? По собственному опыту автора – не меньше пятнадцати минут, причём с определённым навыком устного и письменного счёта. А теперь представим, что эта задача всплыла от звукометристов по ходу контрбатарейной стрельбы. Пока только вычисляем координаты огневых позиций вражеской батареи, она уже успеет наделать дел, своя пехота и свои огневики очутятся в кромешном аду. А потом надо будет делать ещё другие вычислительные и подготовительные операции. То, что спустя полчаса наша контрбатарейная группа откроет огонь и подавит врага будет слабым утешением для своих убитых и искалеченных солдат.
Для приведённой выше картинки уже в числовом выражении: Xa = 1000, Ya = 1000, Xb = 2000, Yb = 6000, буссоль на точку С из пункта А – 04-66, из пункта B – 54-19. Соответственно угол a = 04-66 делений угломера (д.у.) = 466 тыс. = 0,488 рад, угол b = 05-81 д.у. = 581 тыс. = 0,608 рад. Из таблиц находим тангенс угла a = 0,531 и тангенс угла b = 0,696. Теперь с учётом знака «минус» тангенса угла b записываем выражение для Хс:
Хc = (1000*0,531 + 2000*0,696 + 6000 – 2000) / (0,531 + 0,696) = 5642
Yc = (5642 – 1000) * 0,531 + 1000 = 3465
С навыком таких вычислений время расчёта существенно сокращается, кроме того у старых артиллерийских вычислителей были хитрости, как с помощью алгебраических преобразований максимально уменьшить число наиболее затратных операций умножения и в особенности делений. Увы, к 2005 году, когда автор постигал все эти премудрости, эти приёмы уже забылись – всё-таки электронный калькулятор, начиная с 1970-х гг. стал обыденностью, а в машинах управления огнём 1В13, 1В14 и иже с ними появились и полноценные специализированные ЭВМ. Надобность в передаче этих знаний следующим поколениям советских артиллеристов отпала. Но вернёмся таки в прошлое – затратные по времени умножения и деления с помощью таблиц десятичных логарифмов и антилогарифмов приводились к операциям сложения и вычитания. Всё это уже безвозвратно кануло в Лету, но асы-вычислители того периода управлялись со всеми аналитическими расчётами за три минуты с использованием заранее подготовленных шаблонов тех или иных ситуаций. Например, для ряда треугольников, характерных при расположении постов сопряжённого наблюдения или приёмников звукометрических станций заранее табулировались их элементы, а отклонения от эталона приводились в виде поправок «плюс-минус». Так получалось ещё быстрее. Примечательно то, что когда быстродействие ЭВМ было невелико, а расчёт сложной функции занимал много времени, программисты также использовали таблицы её заранее вычисленных значений для интерполяции между ними. Познакомившись с этим, автор уже не удивлялся, почему для обучения артиллерийских вычислителей (также уходящая в прошлое ВУС) РВК потребовал именно лиц, работающих программистами (должности у них были правда разные, но суть была именно такова). Ну и попутно: «продвинутые» морские системы управления огнём начала 1940-х такую задачу вообще не решали, ибо пункт наблюдения был только один – собственный корабль.
Теперь скажем пару слов и о точности выходного результата. Пусть мы определяем положение точек А и В на местности с погрешностью плюс-минус 12,5 м по данным точной топогеодезической привязки с помощью буссолей и теодолитов, а также использования сети геодезических сигнальных пунктов. На карте масштабом 1:25000 1 см равен 250 м, а 12,5 м на местности будут соответствовать 0,5 мм на карте – вполне в пределах возможностей циркуля и хордоугломера. Считаем, что ошибки измерения всех координат точек распределены по нормальному (гауссовому) закону с вероятным отклонением Е и независимы друг от друга, что вполне выполняется на практике. Раз так, то выходная погрешность определения координат точки С будет:
Ec2 = E2(tg2 a + tg2b + 2) / (tg a – tg b)2;
(Е. С. Венцель, «Теория вероятностей», формула 12.7.4 на стр. 279, изд. 1964 г.)
в числах это будет так: Ec = 12,5 * sqrt((0,5312 + 0,6962 + 2) / (0,531 + 0,696)2) = 17 м
Поэтому понятны рекомендации выбирать позиции постов сопряжённого наблюдения или приёмников звукометрической станции относительно предполагаемого местонахождения цели так, чтобы тангенсы соответствующих углов по модулю были меньше единицы, а их разность – больше единицы. Иначе получим слишком большой «плюс-минус» в определении координат точки C, который ещё увеличит погрешность последующих вычислений топографической дальности до цели. В нашем примере определение Хc и Yc с погрешностью около плюс-минус 20 м вполне себе приемлемо, т. к. вероятное отклонение по дальности из-за рассеивания у 122-мм пушки А-19 на дистанции, к примеру, 10 км составляет 50 м. Какой бы ни была погрешность вычисления координат цели, она всё равно гарантированно попадёт в срединную полосу по дальности, если огневые данные рассчитаны правильно. Такого рода оценки тоже входят в обязанности артиллерийского вычислителя, поскольку из них вытекает вероятность поражения цели и расчёт надлежащего для того количества выстреливаемых снарядов.
Была ли какая-нибудь альтернатива таким точным вычислениям на бумаге в годы Великой Отечественной войны? Увы, не было. Но можно ли было помочь в вычислениях, чтобы уменьшить вероятность появления в них ошибки помимо совершенствования чисто алгоритмических методов счёта? А вот тут да, причём внимание – с использованием переносных цифровых вычислительных машин! Но не двоичных электронных, а десятичных механических. В документах некоторых пушечных артиллерийских полков и бригад упоминаются расчёты с применением арифмометра «Феликс». Это устройство вполне себе мобильно, по габаритам и массе сравнимо с миниатюрной пишущей машинкой, которая полагалась по штату артиллерийской части, и позволяло выполнять операции сложения, вычитания, умножения и деления с весьма высокой точностью за разумное время.
Это было особенно важно для звукометристов, а также огневиков при задействовании метода полной подготовки данных для стрельбы или при нехватке снарядов, когда пристрелка будет расточительством последних.
Но если есть возможность контроля отклонений разрывов от цели и снарядов достаточно, то можно понизить допустимую точность вычисления огневых данных. Возможный уход области разрывов от желаемой точки на местности вследствие погрешностей в исходных данных и алгоритмах расчётов будет компенсирован пристрелкой. В таком случае вместо точных аналитических построений можно использовать графический метод решения описанной выше задачи либо на листе миллиметровки или тетрадной клетчатой бумаги, либо используя артиллерийский круг.

Артиллерийский круг в экспозиции Военно-исторического музея артиллерии, инженерных войск и войск связи, г. Санкт-Петербург
Из последнего, кстати, вырос известный каждому вычислителю в 1970-х – 2000-х гг. механический прибор управления огнём ПУО-9, позволяющий быстро переходить от полярных координат к декартовым и обратно. Эта довольно габаритная вещь, внешне похожая на металлическую раскладную шахматную доску с подвижной по ней поворачивающейся линейкой с угломерной шкалой, сейчас уже активно заменяется электронными планшетами, но, по идее, она должна остаться резервным средством. Было бы глупо идти в турпоход в лесную глушь только с GPS/ГЛОНАСС навигатором без карты и компаса: вдруг это устройство откажет или врать начнёт. На практике в родном городе автора этих заметок маршрутные автобусы на информационных экранах остановок общественного транспорта одно время ездили по дну Оки и имели чудодейственное свойство проходить через стены зданий. Во время отдыха на борту т/х «Михаил Фрунзе» смартфон одного из попутчиков уверенно сообщал, что судно плывёт не по Горьковскому водохранилищу, а перемещается по сухопутной дороге, ведущей в Чкаловск. Так и у артиллеристов – аккумуляторы в планшете разрядятся, ошибка программистов в его коде обнаружится, цифровая карта местности – форменный отстой или противник средствами РЭБ сделает работу устройства бесполезной. Так что отправлять старые проверенные методы вычислений в архив ещё рановато.
Если не нужно большое число точных цифр в результате, то резко ускорить вычисления позволяет такая аналоговая вычислительная машина как логарифмическая линейка. Собственно говоря, на снимке из серии про работу звукометристов мы её и видим в руках советских солдат:

Советские звукометристы за работой. Снимок из экспозиции Военно-исторического музея артиллерии, инженерных войск и войск связи в Санкт-Петербурге
С использованием принципа действия логарифмической линейки были разработаны такие приборы как метеобаллистический сумматор для 152-мм гаубицы-пушки МЛ-20 (автор самолично видел такой, когда носил «трёхцветку» с чистым погоном) и приборы расчёта корректур. Разновидность последнего ПРК-69 пришлось вместе с нашим взводным осваивать самим, благо на нём было написано, как его использовать. Лейтенанта И. в Казанском артиллерийском училище работе с таким антиквариатом уже не обучали (использовался более поздний ПРК-75 и электронные средства). Что же касается рядового С., то на время занятий с ПРК-69 ему «повезло» из «партизана» вынужденно на неделю переквалифицироваться в «трёхсотого» с нахождением в медчасти. Лирическое отступление: кормёжка там была, кстати, по качеству продуктов и работе повара лучше иной ресторанной, с солдатской столовой вообще не сравнить. В посудомоечной контролёром по этой части нёс свою нелёгкую службу медчастный пушистый и упитанный кот. Днём он выборочно проверял еду, свернувшись колобком, наблюдал за процессом мойки посуды, а по ночам отправлялся в самоволку, часто с последующим его розыском офицерским составом медчасти. Но (заканчиваем экскурс в воспоминания) животворящий пенициллин позволил автору за неделю вернуться в строй и освоить ПРК-69. Начальник штаба батареи сборов и выпускник Михайловской академии майор Т. так быстро с ним работал, что автору, уже при наличии калькулятора, было с ним не тягаться в скорости расчёта корректур при пристрелке. Эта задача выполнялась им при известных данных где-то за полминуты! И каково же было удивление, когда в питерском Артиллерийском музее автор увидел вот это:

«Счислитель» в экспозиции Военно-исторического музея артиллерии, инженерных войск и войск связи, г. Санкт-Петербург
Эта вещь есть ни много ни мало как ПРК-69, только сделанный полукустарно. Т. е. методы механизации приближённых вычислений, специфичных для артиллерии, уже активно применялись в Великую Отечественную войну! Стоит заметить, что гитлеровская артиллерия по состоянию на конец 1941 год особо не любила аналитику и подобные средства, предпочитая использовать хитрым образом составленные номограммы и графики. Наши профильные специалисты отметили их удобство использования, но посетовали на низкую точность и пошли своим путём. Аппарат номограмм в советской артиллерии использовался мало. В этом плане удивительно, что при высокоразвитой германской научной математической школе гитлеровцы во многих связанных с ней областях существенно проиграли своим противникам из США, СССР и Великобритании. Таким образом, от материальной части 122-мм пушек А-19, средств артиллерийской разведки и управления огнём мы плавно пришли к главному вопросу – насколько были под всё это готовы кадры от высокопоставленных командующих до нижних чинов. Ибо без знающих и умелых людей вся эта техника бесполезна. Но об этом в следующий раз, эта серия и без того получилось где-то раза в два больше, чем обычно.
источник: https://afirsov.livejournal.com/659726.html







А сварка в то время была уже на таком уровне? Сварной корпус мины, приваренные стабилизаторы…
++++++++++
++++
Спасибо за качественные и подробные фотографии.
Нравится мне вот такое неказистое и незнаменитое оружие.
Еще хотелось бы ТТХ узнать, об истории применения почитать, особенно меня интересует процент снаряжения мин.