Еще одна интересная статья из жж Андрея Фирсова.
Текст Анатолия Сорокина
Поскольку в рамках обсуждения поста «Пора добраться до шрапнели» было высказано весьма справедливое замечание о наличии особенности в зависимости плотности вероятности от направления в пространстве при используемом алгоритме генерации угла отклонения, надо было «провентилировать» возникшую ситуацию. Она оказалась не слишком-то хорошей (Майн готт, Карл, особенность-то неинтегрируемая, аллес капутт! Вир зинд ферлорен!): при нулевом угле отклонения F от оси симметрии боеприпаса и стремлении малого интервала dF по этому углу к нулю вероятность P попасть в этот интервал равна C*dF, где С – некая константа, а телесный угол, образуемый конусом с углом раскрыва dF пропорционален dF2. А дальнейшее очевидно: плотность вероятности в пересчёте на телесный угол пропорциональна 1/dF – стремится к бесконечности и по ней нельзя взять конечный интеграл.
Поэтому в улучшенном алгоритме моделирования вместо равномерного распределения по углу F плотность вероятности была взята линейно возрастающей от нуля до половинного раскрыва конуса разлёта поражающих элементов. Таким образом, вблизи нуля P = k * dF2, особенность устранена, плотность вероятности на оси симметрии равна какому-то конечному значению. Такая модель имеет и физический смысл: конус разлёта поражающих элементов обуславливается центробежной силой (если система отсчёта неинерциальна и связана с вращающимся боеприпасом), которая тем больше, чем дальше находится пуля или «иголка» от оси симметрии боеприпаса. А чем больше расстояние от оси, тем больше пуль или «иголок» (причём в линейной зависимости) находится на соответствующем ему удалении.
Условия задачи также претерпели изменения: на горизонте орудия на расстоянии 7 км от его огневой позиции находится одиночный пехотинец противника. Найти вероятность их поражения одним выстрелом для 122-мм гаубицы обр. 1938 г. (М-30) снарядом с готовыми стреловидными поражающими элементами Ш1 с дистанционной трубкой 45 с (для М-30 шрапнель не предусмотрена).
Установки прицела и угломера выставлены так, что средняя траектория по их пучку проходит прямо через ростовую фигуру цели (горизонтальную проекцию вертолёта). Табличная установка трубки рассчитана на инициирование её действия на заданном удалении от цели.
Данные из таблиц стрельбы:
Начальная скорость боеприпаса V0 на полном заряде: 515 м/с
Время полёта до цели tC: 21 с
Оконечная скорость боеприпаса VC: 270 м/с
Угол падения относительно плоскости горизонта орудия: θС: 22 гр.
Вероятное отклонение по дальности ВД: 41 м
Вероятное отклонение по фронту (боковое) ВБ: 2,8 м
Вероятное отклонение по высоте ВВ: 16 м
Количество «иголок» в боеприпасе: 6000
Угол разлёта «иголок» β: 20 гр.
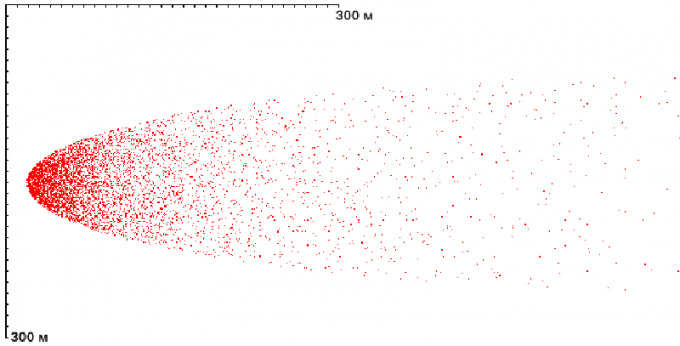
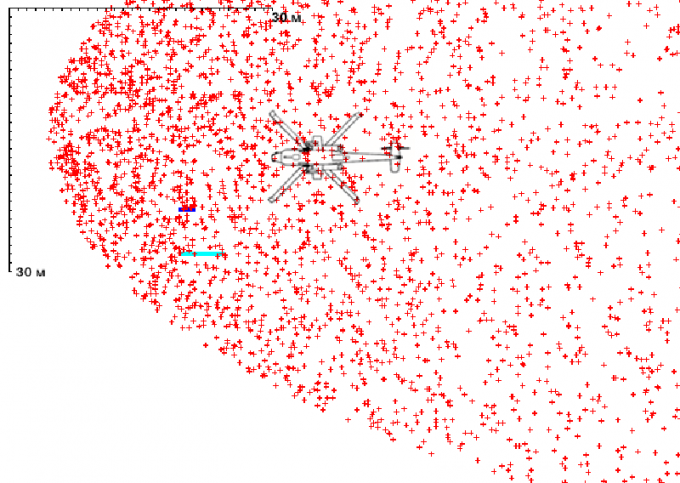
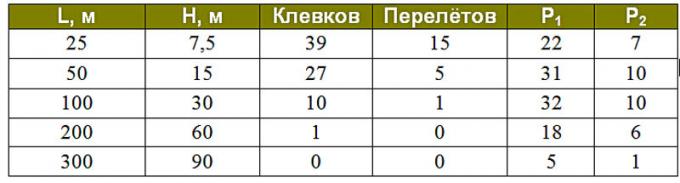
Результаты моделирования приведены в таблице и на двух рисунках.
На первом из них изображены красными точками попадания «иголок» на плоскость горизонта орудия, на второй – фрагмент этой плоскости в более крупном масштабе, где светло-синим обозначена проекция стоящего прямоугольника 170 × 40 см, имитирующего стоящего пехотинца, при попадании в которую цель считается поражённой. Синим цветом показан тот же прямоугольник, имитирующий залёгшего пехотинца и «по просьбам читателей» обозначен силуэт некоего вертолёта для оценки числа попаданий в него «иголок». Известно, что на дистанции 200 м стреловидный поражающий элемент от Ш1 надёжно пробивает армейский бронежилет и стальной шлем эпохи начала 1980-х гг. Однако есть сомнения, что он способен нанести существенный ущерб вертолёту.
Где L – планируемое удаление точки разрыва снаряда Ш1 от цели по дальности на горизонтальной плоскости;
H – планируемая высота точки разрыва;
P1 – число поразивших стоящую цель выстрелов хотя бы одной «иголкой» из сотни, грубая оценка вероятности этого события в процентах;
P2 – число поразивших лежащую цель выстрелов хотя бы одной «иголкой» из сотни, грубая оценка вероятности этого события в процентах.
Заметим, что при отсутствии рассеивания снарядов и «подводе» цели под наиболее «плотный» «дождь» «иголок» даже на 7 км «стоящая» вероятность поражения превышает 95%. Прочие выводы оставляю читателям.
Самому же хочется отметить один методологический аспект из теории и практики (пардон за тавтологию) теории вероятностей. Для преобразования равномерно распределённой случайной величины в интервале от 0 до 1 в «половинку» распределения Симпсона (когда плотность вероятности случайной величины X прямо пропорциональна самой этой величине – на интервале от 0 до 1 она будет равна 2*х) надо, очевидно, применить к ней некоторое функциональное преобразование. В любом учебнике тервера эта задача освещена: на случайную величину надо подействовать обратной к желаемой плотности вероятности функцией. К примеру, хотим экспоненциальное распределение – действуем минус логарифмом. Но обратная функция к 2*х – это х/2, а любое линейное преобразование равномерно распределённой случайной величины оставляет её … правильно, равномерно распределённой, но в другом интервале значений. Так как же получить «полСимпсона»? Под стук трамвайных колёс по дороге домой долго думал, вспоминая студенческие годы, второй семестр второго курса. Вот здесь пришлось выбросить белый флаг – т. е. обратиться к Е. С. Вентцель – там ответ и алгоритм действий для получения желаемого результата приведён.
источник: https://afirsov.livejournal.com/280521.html