Еще одна интересная статья из жж Андрея Фирсова.
Текст Анатолия Сорокина
Для защиты свободы и мира
Есть гранаты, готова шрапнель,
Наши пушки и наши мортиры
Бьют без промаха в цель!
Марш артиллеристов, 1938 г
После публикации о действии осколочно-фугасного снаряда (ОФС) при стрельбе по удалённому на 4 км одиночному солдату противника («Трубка 15, прицел 120, батарея! Бац-бац! И … мимо» (с)) в одном из комментариев возник вопрос, а что было бы при использовании шрапнели? Тема эта оказалась интересной сразу с нескольких точек зрения, поэтому пришлось изрядно вспомнить тригонометрию и посидеть пару часов над бумагой и таблицами стрельбы, чтобы разобраться, что к чему. Заметим, что аналогичный этап для ОФС не занял и пяти минут – перед тем, как закладывать формулы и значения в программу моделирования огня. Хорошая иллюстрация, почему шрапнель «тихой сапой» в межвоенное время стала исчезать из артиллерийской практики – а ведь тогда не было в помощь ни компьютера, ни калькулятора, а быстроте и точности счёта на логарифмической линейке надо было учиться неделями. Арифмометры типа «Феликса» по целому ряду причин решением для полевой артиллерии не были, хотя производные от них – механические или электромеханические счётные машины – прижились на крупных артиллерийских кораблях.
В отличие от ОФС с ударным взрывателем шрапнель времён Великой Отечественной войны является дистанционно подрываемым (с точки зрения совершенно строгих правил и определений – подрываемым по пиротехническому таймеру внутри трубки) боеприпасом и точки подрыва разбросаны не по какой-то области на плоскости, а в некотором объёме трёхмерного пространства. Но это ещё полбеды, поскольку также приводятся в действие и ОФС с дистанционным взрывателем – в те годы их называли бризантными гранатами. В последнем случае более сложной становится картина распределения точек разрывов, но по-прежнему основную роль играет удаление цели от места разрыва бризантной гранаты при расчёте поражения осколками и ударной волной. При этом ударная волна «разбегается» изотропно от точки своего возникновения, а осколки летят и вперёд, и назад, и по сторонам, и вниз, и вверх, хотя и неравномерно по всем направлениям. Но если ОФС разорвался в воздухе не далее чем в 10 м от цели, то её можно считать уничтоженной с гарантией. А шрапнель характеризуется тем, что поражает цель пулями, выброшенными из неё в определённом (и довольно узком) телесном угле по направлению её полёта, а вне него из-за малости вышибного заряда её действие ничтожно. И это кардинально меняет дело! Но перед тем, как перейти к числам, напомним условия задачи и характеристики системы.

Расчёт 122-мм гаубицы обр. 1909/37 гг. Один из номеров держит в руках шрапнельный боеприпас, легко опознающийся по кольцу предохранительной чеки трубки
Условия задачи: на горизонте орудия на расстоянии 4 км от его огневой позиции находится одиночный пехотинец противника. Найти вероятность его поражения одним выстрелом для 122-мм гаубицы обр. 1910/30 гг. или 122-мм гаубицы обр. 1909/37 гг. (их баллистика идентична) шрапнелью Ш-460 с трубкой 45 с (для М-30 шрапнель не предусмотрена). Установки прицела и угломера выставлены так, что средняя траектория по их пучку проходит прямо через ростовую фигуру цели. Табличная установка трубки шрапнели рассчитана на инициирование её действие на горизонте орудия.
Данные из таблиц стрельбы:
Начальная скорость боеприпаса V0 на полном заряде: 343 м/с
Время полёта до цели tC: 14,8 с
Оконечная скорость боеприпаса VC: 240 м/с
Угол падения относительно плоскости горизонта орудия: θС: 16 гр. 18 мин.
Вероятное отклонение по дальности ВД: 27 м
Вероятное отклонение по фронту (боковое) ВБ: 2,2 м
Вероятное отклонение по высоте ВВ: 7,5 м
Количество пуль в боеприпасе: 550
Угол разлёта пуль β: 15 гр.
Сразу видно, что, манипулируя установкой трубки, надо добиться разрыва шрапнели в воздухе на некотором удалении перед целью, иначе, стоит боеприпасу перелететь на какой-то метр дальше цели или совершить «клевок» перед ней из-за неизбежного рассеивания при стрельбе, поражения не будет вовсе – цель не попадёт в конус разлёта пуль. Шанс же зацепить её стаканом (который не дробится на осколки), стержнем или слабенькой ударной волной от сотни грамм дымного пороха просто ничтожен. Прикидывая те или иные варианты в течение тех двух часов, пришёл к выводу, что есть некоторая оптимальная точка разрыва шрапнели впереди цели: тогда, как бы она не «гуляла» по дальности и фронту, пехотинец хоть стоя, хоть лёжа попадает в конус разлёта пуль. С рассеиванием по высоте всё сложнее, т. к. при больших отклонениях вверх или вниз (более 2ВВ) цель выпадает из конуса поражения. Чтобы обеспечить гарантированный её захват, надо ещё более повышать и удалять от неё точку разрыва, а это ведёт к резкому падению шанса попадания в ростовую фигуру (хоть стоящую, хоть лежащую) пуль из-за снижения плотности их потока. Кроме того, при начальной скорости крупных (диаметр 13,25 мм) шарообразных пуль в 240 м/с массой 19,2 г (вышибной заряд у Ш-460 не придаёт им сколь-нибудь значительной добавки в скорости) сопротивление воздуха быстро выводит их действие за рамки «убойности». Поэтому увеличивать дистанцию от точки разрыва шрапнели до цели свыше 300–400 м нельзя. А приближать её ближе 50 м (высота разрыва 15 м) тоже нельзя, ибо тогда резко увеличивается шанс на клевок или перелёт, при этом значительно сужается и область пространства, захватываемая конусом разлёта пуль. На этом собственно можно вводить данные в программу численного моделирования стрельбы методом Монте-Карло, ибо аналитический расчёт тут весьма затруднён и фактически требует высшей математики (интегрирование по области рассеивания размазанной по ней и зависящей сложным образом от положения в ней вероятности поражения цели). Численная модель достаточно близка к реальности – внутри конуса поражения вектора скоростей пуль распределены по углу отклонения от направления полёта от –β/2 до +β/2 с некоторым тяготением к нулю и равномерно по азимутальному углу в перпендикулярной направлению плоскости от 0 до 2π.
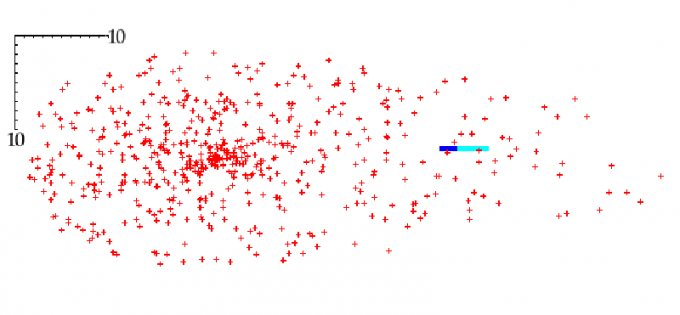
После пересчёта из одной системы координат в другую (аналитическая геометрия и высшая алгебра, уровень 1-й курса матфаков, физфаков, радиофаков, мехматов и т. п. плюс 11-х классов физматлицеев и физматгимназий) в итоге смотрим попадания пуль в область, соответствующую проекции цели на горизонтальной плоскости (при положении пехотинца лёжа – фактически в саму цель).
— результат численного эксперимента. Красными крестиками показаны места падения 550 пуль на плоскость горизонта орудия, шкала расстояний указана в метрах. Светло-синим цветом показана проекция вертикально стоящего прямоугольника размером 170 на 40 см, имитирующего стоящего пехотинца, при попадании в которую цель считается поражённой. В ходе моделирования получилось одно пересечение траекторией пули этого прямоугольника. Синим показан тот же прямоугольник на плоскости горизонта орудия, соответствующий лежащему пехотинцу. Имеются два близких попадания, но цель в этих условиях осталась непоражённой. Отметим, что из-за дозвуковой скорости шрапнели на траектории в тихой обстановке вражеский пехотинец может сначала услышать звук выстрела гаубицы и «шелест» приближающегося боеприпаса, время на залегание в таком случае у него есть.
Эти формулы приводить здесь не будем, желающие могут их вывести в порядке небольшой гимнастики ума и реминисценций позднешкольных или студенческих (курсантских) лет в области тригонометрии. Перейдём сразу к оконечному результату. На каждой из установок трубки было произведено 100 виртуальных выстрелов столь же виртуальной шрапнелью Ш-460 (10 часов в реальности при медленном темпе огня в 1 выстрел в минуту при исправлении наводки и пробанивании ствола после каждого выстрела плюс перевозка 300 ящиков с боеприпасами общей массой около 25 т – достаточное основание, чтобы баллистически перепроверять на практике таблицы стрельбы раз в пять лет, если не реже).
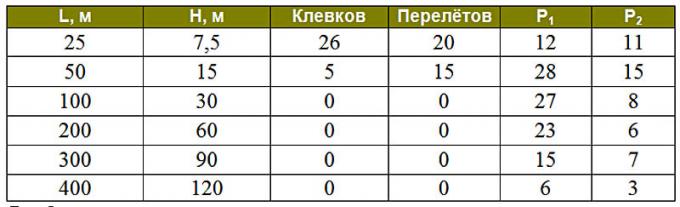
Где L – планируемое удаление точки разрыва шрапнели от цели по дальности на горизонтальной плоскости;
H – планируемая высота точки разрыва шрапнели;
P1 – число поражений стоящей цели, грубая оценка вероятности этого события в процентах;
P2 – число поражений лежащей цели, грубая оценка вероятности этого события в процентах.
Вывод из всего вышеизложенного один – автор уже не в первый раз оказался в положении Капитана Очевидность, подтвердив эффективность шрапнели против открыто расположенной живой силы противника со всеми сопутствующими оговорками: негодность против любой фортификации, слабое по сравнению с ОФС действие по бронецелям, дороговизна и сложность изготовления, неудобство в применении. Удивительно другое: в конце 1930-х гг., подчёркивая эти факторы в памятках, наставлениях и уставах, для новых гаубиц М-30 и М-10 шрапнель вывели за рамки боекомплекта и в таблицах стрельбы для них соответствующих разделов просто не было. Но познакомившись с ситуациями, когда на десятерых наших прёт «многое множество есть бесчисленно» солдат вероятного противника в плотном строю с криками «Банзай!» или что-то типа того, к счастью, всё-таки сделали 122-мм снаряд со стреловидными готовыми поражающими элементами 3Ш1 и 152-мм аналог 3Ш2. Иногда на вышеупомянутого «Кэпа» всё-таки стоит обращать внимание.
источник: https://afirsov.livejournal.com/278763.html
Часть 2