О таблицах стрельбы, часть IVб (снова таблицы стрельбы большей частью отсутствуют)

Статья из жж Андрея Фирсова.

Текст Анатолия Сорокина

Рассмотрим такую ситуацию: артиллерийское орудие ведёт огонь по наземной цели с корректировкой результатов стрельбы при помощи воздушного наблюдения (пилотируемый экипажем или дистанционно летательный аппарат). Разрывы ложатся где-то недалеко от цели, необходимо точно вывести их область в желаемое место. Сделать это можно путём изменения установок стрельбы: угла возвышения ствола (т. е. соответствующего ему значения прицела по-артиллерийски) и дирекционного угла (а здесь значения угломера на языке Бога войны). А если посмотреть на это с точки зрения математики вообще и математического анализа в частности? Вспоминаем часть IVа, её фрагмент про «превращения» одних числовых величин в другие, и получаем следующее:

X = Fx(А, B)
Y = Fy(А, B)

Где Х, Y – координаты центра области разрывов, A – значение прицела, B – значение угломера. Величины А и В посредством системы «артиллерийское орудие–боеприпас–атмосферные условия–рельеф местности» в реальности, т. е. функций Fx и Fy в математике, преобразуются в X и Y. Так вот, с точки зрения «чистого» математика для решения поставленной задачи нам надо спросить лишь одно: дифференцируемы ли функции Fx и Fy по своим аргументам А и В? Насчёт офицера-артиллериста, выпускника военного училища, а то и академии, в теории можно сказать, что он должен дать ответ на этот вопрос (ибо математический анализ входит в программу его обучения). И этот ответ прост: да, эти функции дифференцируемы по обоим своим аргументам. То есть любое малое изменение аргументов в окрестности какой-то точки влечёт за собой прямо пропорциональное им малое изменение значений этих функций с пренебрежимой на практике добавкой «кривизны» (вспоминаем другой фрагмент части IVа, про параболу «икс квадрат» и прямую «два икс минус один» в окрестности точки «икс равно одному»).

И всё, математику этого достаточно, не надо знать ничего про тысячные или угловые минуты, метры или сажени, он вообще оперирует абстрактными безразмерными величинами. Алгоритм тут таков: пусть ΔX и ΔY – отклонения центра области разрывов от желаемой точки. ΔX возьмём за одну условную единицу дальности, «у.е.» и через неё выразим ΔY. А потом попросим (математик – гражданский человек, командовать военными не имеет права) расчёт орудия дать две серии выстрелов.

В первой серии выстрелов пусть расчёт увеличит значение прицела А «на такую малость dA, которую этот его прицел позволяет» (0,5 тысячных или 1,8 угл. минуты на практике) и оставит угломер В неизменным. Во второй серии выстрелов математик скажет расчёту сделать то же самое с угломером В (практическая точность dB та же, полцены деления соответствующей шкалы на артиллерийской панораме) и оставить прицел А неизменным. Так практическим путём получим, что, например, изменение прицела на «одну малость dA» при фиксированном угломере приводит к изменению координат dX центра области разрывов по оси Х на сколько-то «у.е» и на сколько-то «у.е.» dY по оси Y. Такая же картина, но с другими величинами в «у.е.» dX и dY случится при изменении угломера на «одну малость dB» при фиксированном прицеле. Всё это есть следствие математического факта дифференцируемости соответствующих функций:

dX = ∂Fx/∂A×dA + ∂Fx/∂B×dB
dY = ∂Fy/∂A×dA + ∂Fy/∂B×dB

Так, практическим путём, мы находим числовые значения коэффициентов перед dA и dB. При малом изменении прицела и фиксированном угломере dA = 1 и dB = 0, а при малом изменении угломера всё наоборот: dA = 0 и dB = 1, а измеренные в «у.е.» dX и dY сообщит нам воздушный наблюдатель. «Жуткая» запись этих коэффициентов ∂Fx/∂A, ∂Fx/∂B, ∂Fy/∂A, ∂Fy/∂B вызвана тем фактом, что они есть значения частных производных в окрестности точки центра области недалёких разрывов от цели (т. н. «точки накола»). Что такое частная производная – это уже сюда: www.mathprofi.ru/chastnye_proizvodnye_primery.html . По-простому же – насколько пропорционально изменение функции от нескольких переменных изменению «на одну малость» конкретного её аргумента при фиксации всех прочих в какой-то точке. В нашем случае, например, увеличил наводчик угол возвышения на одну тысячную и область разрывов отклонилась в сторону увеличения своей координаты Х на 30 метров. Это и будет значением ∂Fx/∂A в реальных физических единицах измерения вместо абстрактных «малостей» и «у.е.» И важно, что для нас в практическом смысле это какое-то число. А дальше меняем d на Δ:

ΔX = ∂Fx/∂A×ΔA + ∂Fx/∂B×ΔB
ΔY = ∂Fy/∂A×ΔA + ∂Fy/∂B×ΔB

Значения ∂Fx/∂A, ∂Fx/∂B, ∂Fy/∂A, ∂Fy/∂B нами практическим путём определены, ΔХ и ΔY – известны по результатам изначального воздушного наблюдения. Что имеем относительно ΔА и ΔВ? Правильно, тривиальную систему двух линейных уравнений с двумя неизвестными, которую в старших классах школы учат решать. Решаем её и получаем рецепт совмещения центра области разрывов с целью. Например, математик скажет расчёту после определения ΔА и ΔВ: «вам, ребята, надо к прицелу добавить три «малости», а от угломера вычесть одну». И цель будет накрыта! Правда, этот метод корректировки огня жутчайше неэффективен по расходу снарядов.

При стандартной для артиллерийской практики пристрелочной серии в четыре выстрела на всю процедуру придётся потратить как минимум 12 снарядов. Четыре из них придутся на «точку накола», четыре на определение отклонения по прицелу при фиксированном угломере, ещё четыре – на определение отклонения по угломеру при фиксированном прицеле. Только потом можно вести огонь на поражение, да и то, если «точка накола» оказалась недалеко от цели. В противном случае потребуется ещё один подобный шаг (фактически это применение метода Ньютона нахождения нулей функции на практике). «В поле» так почти никогда не делают – таблицы стрельбы как раз содержат в себе данные, нужные для переноса огня. Но получены они не только теоретическими выкладками, но и опытным отстрелом артиллерийской системы на полигоне с целью уточнения математической модели движения снаряда в воздушной среде. Там как раз в некоторых контрольных точках описанная процедура применительно к дальности и проводится, чтобы в поле по известным данным быстро переносить огонь в нужное место от пристрелянных заранее точек (реперов) или от не совсем точного, но близкого попадания в окрестность цели.

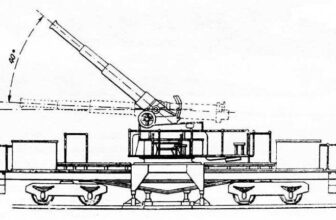
Например, для показанной на заглавном снимке 152-мм гаубицы обр. 1938 г. (М-10) известно, что на первом заряде в диапазоне дальностей от 4 до 4,2 км изменение прицела на 1 тысячную (та самая «малость») вызывает смещение точки пересечения траектории снаряда с горизонтом орудия по дальности на 23 метра (причём от погодных условий и прочих характеристик стрельбы эта величина практически не зависит). Если ось Х направлена вдоль линии огня, а ось Y – перпендикулярно к ней, то эти 23 метра (на тысячную) есть не что иное, как значение упомянутой выше частной производной ∂Fx/∂A в диапазоне значений её аргумента А от 129 тыс. (соответствует дальности 4 км) до 138 тыс. (соответствует 4,2 км). То есть мы можем сразу же (при предельно упрощённом рассмотрении, конечно), помочь расчёту М-10 решить такую боевую задачу:

Цель – ДЗОТ врага удалён на 4000 м строго на север от огневой позиции нашей гаубицы М-10. Времени на точное измерение параметров орудия, атмосферы и снарядов/зарядов нет, но погода безветренная и нам в помощь самолёт-корректировщик У-2. По таблицам стрельбы даём установку прицела 129 для заряда первого (хотя тут и восьмым обойтись можно, но пусть так) по шкале тысячных и установку буссоли (дирекционного угла) в 59-56 (снаряд из-за деривации уклоняется вправо на 4 тысячных для указанной дистанции, так что ствол должен быть повёрнут чуть левее на этот угол, а угломер зависит от того, на какой ориентир головка панорамы смотрит, вовсе не обязательно по направлению стрельбы). Стреляем четыре раза (хотя, может быть, для такой дистанции достаточно и одного снаряда – рассеивание тут небольшое), летнаб сообщает – область разрывов по направлению верно, но южнее цели на 50 метров. То ли холодно стало и атмосфера стала более плотной, то ли у орудия существенен разгар каморы, то ли снаряды лёгкие, чем по стандарту, попались, в общем что-то стало причиной недолёта, разбираться некогда! Но зная значение ∂Fx/∂A, нам это не станет проблемой: командуем установку прицела 131 (+2 тысячных даёт увеличение дальности на 46 метров) и сразу же начинаем беглый огонь на разрушение цели.

В наше время всё это запрограммировано в системе АСУНО российской артиллерии. Оснащённые ей наши современные системы способны дать один выстрел для «точки накола», а затем, рассчитав значения всех упомянутых выше производных, сразу переходить на поражение цели. Этому способствует уменьшившееся рассеивание снарядов из-за улучшения технологии их производства: на роботизированных линиях гораздо лучше выдерживаются масса, размеры и форма по чертежу боеприпаса, надлежащая форма чистовой обработки его поверхности. Человеку-рабочему так ровно изготовить их очень трудно. Но вернёмся к АСУНО: данные в неё автоматически поступают и от метеостанций, и от систем, контролирующих работу орудия, и от ДПЛА, ведущих наблюдение за целью. При необходимости можно с терминала эту информацию ввести также вручную. А дальше – вся вот эта описанная выше математика, скрытая в программном и аппаратном электронном обеспечении компонент АСУНО. За справками – к ребе Кацману (https://t.me/s/pozivnoy_kazman), у него много материалов по работе и системам управления огнём современной российской артиллерии. Автор со своей старой схемой с живым вычислителем (на которого его когда-то и учили) безнадёжно отстал во времени. Он может лишь сказать, что и человек делает то же самое, только не так быстро и с более вероятными ошибками в процессе своей работы (у артиллеристов немало баек, когда из-за вычислителей или плохого канала связи от передового наблюдателя снаряды уходили не туда, куда нужно с последствиями от комических до трагических).

И вот из-за последнего фактора всплывает упомянутое «почти никогда не применяется» касательно рассмотренной нами выше умозрительной схемы корректировки огня абстрактным математиком. Дело в том, что управление огнём, хоть через АСУНО, хоть старомодным вычислителем – довольно сложная вещь и в ней возможны ошибки. Эти последние могут быть и алгоритмическими («софт», «железо» и мозг вычислителя могут «глючить»), могут и содержаться в некорректных исходных данных (например, забыли про разность высот орудия и цели или – проблемы будут: таблицы стрельбы говорят одно, а на практике получается совсем по-другому). И вот тогда такая «тупая» схема с большим расходом снарядов вполне может решить поставленную задачу, если у нас таблиц стрельбы нет вообще или с их использованием (хоть книгой, хоть в АСУНО) какая-то лажа получается. Главное, лишь бы наблюдатель засёк «точку накола» недалеко от цели. Также примечательно во всём этом то, что и последнее условие можно выполнить без таблиц стрельбы, зная лишь некоторые математические свойства функции зависимости дальности стрельбы от угла возвышения. Но об этом в следующий раз.

источник: https://afirsov.livejournal.com/937327.html