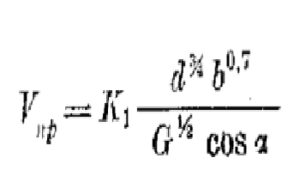Данная статья предназначена исключительно задать самые первые, самые простые и самые наивные из вопросов относительно формулы пробития брони Жакоба де Марра, точности результатов, полученных путем её применения уважаемыми коллегами к данным в отношении опытовых стрельб, а также корректности экстраполяции таких результатов на условия реальных или гипотетических боев.
Статья написана за сутки при помощи «оперативной памяти» и картинок из популярной литературы, представляет собой наивное обращение любителя к специалистам, поэтому упрощена до примитивизма, как в отношении речи, так и в отношении содержания, при этом содержит определенный объем шуток и троллинга, за которые заранее прошу прощения у читателей. Ни на что кроме попытки немного поджечь стул данная статья не претендует.
Содержание:
Методическая основа вопроса
В соответствии с давно уже не имеющим грифа «Курсом морской тактики. Артиллерия и броня» проф. кафедры артиллерийской стрельбы Факультета военно-морского оружия Гончаров Л.Г. (издание Военно-Морской Академии РККА им. тов. Ворошилова, Л. — 1932) для расчета пробития брони используется формула Жакоба де Марра
которая в формате Excel может быть записана следующим образом:
V = K*(d^0,75*b^0,7)/(G^0,5*cos a)
где:
V – скорость, необходимая и достаточная для пробития снарядом брони в целом (способном к разрыву от штатного взрывателя) виде в метрах в секунду,
К – коэффициент, зависящий от относительного качества между собой брони и снаряда,
d – калибр (диаметр) снаряда в дециметрах,
b – толщина пробиваемой брони в дециметрах,
G – вес снаряда в килограммах,
a – угол встречи снаряда с броней, считая от нормали в градусах,
Эта формула может быть записана с определенными отличиями, но мы берем ее так, как она представлена именно для метрической системы мер именно в указанной книге Гончарова.
Физический смысл формулы пробития брони Жакоба де Марра можно объяснить следующим образом:
выражение V = d^0,75/G^0,5 является по сути классической формулой кинетической энергии E = mv^2/2 с учетом распределения усилия на площадь взаимодействия тел (см. поперечная нагрузка снаряда),
поэтому К представляет собой введенный Жакобом де Марром эмпирической коэффициент для перевода распределенной на площадь взаимодействия тел кинетической энергии в конкретное значение пробития брони, такой коэффициент будет самостоятельным значением, уникальным для каждой конкретной пары «снаряд и броня».
Практический смысл формулы пробития брони Жакоба де Марра можно объяснить следующим образом:
заранее известны d (калибр снаряда) и G (вес снаряда), в ходе испытаний задаются V (скорость снаряда) и a (угол прицеливания),
если сделать один реальный выстрел («эмпирический выстрел»), то узнав по его результатам b (толщину пробиваемой брони) можно рассчитать К (коэффициент, зависящий от относительного качества между собой брони и снаряда),
при необходимости узнать b (толщину пробиваемой брони) для некоего «теоретического выстрела» необходимо определить скорость и траекторию снаряда для такого выстрела в момент встречи с броней, подставить вес и калибр такого снаряда, подставить определенный «эмпирическим выстрелом» К.
Тут, разумеется, необходимо сделать различные оговорки, тем не менее, считается, что верно определенный коэффициент К дает весьма точные результаты расчета для похожих калибров идентичных по конструкции снарядов и похожих толщин идентичных по конструкции плит брони.
Пока вроде бы все просто и очевидно.
Меня терзают смутные сомнения
Рассмотрим практическое применение формулы в отношении описанных в следующих статьях стрельб
Юры из Хабаровска
https://alternathistory.ru/probit-ili-ne-probit-vot-v-chyom-vopros/
https://alternathistory.ru/probit-ili-ne-probit-otvety-na-voprosy/
Андрея из Челябинска
Обратим внимание на следующий показательный случай:

Одна и та же 15-дм броневая плита Вифлеемского завода.
Одна и та же скорость американского бронебойного 12-дм снаряда, выпущенного из одного и того же орудия.
Один и тот же результат: снаряд пробил плиту и разбился.
Угол прицеливания существенно отличается, следовательно cos a в первом случае округленно равен 0,934 (для 21 градуса), во втором случае он равен 1,000 (для 0 градусов), исходя из такого отличия в исходных данных, конечные результаты стрельбы должны значимо различаться. Но они значимо не различаются.
Поскольку иные данные для стрельбы не отличаются настолько, чтобы объяснить феномен, возник продолжающийся несколько статей подряд спор, как правильно определить введенный Жакобом де Марром эмпирической коэффициент для этого конкретно случая – по максимальному значению угла встречи (21 градус) или по минимальному значению угла встречи (0 градусов).
Не вдаваясь в детали спора, подумаем, возможно ли иначе интерпретировать полученные данные.
Как было указано выше, заранее известны d (калибр снаряда) и G (вес снаряда), в ходе опыта подтверждена b (толщина пробиваемой брони).
Возможно ли предположить ошибку в определении V (скорости)? – нет, одна и та же пушка, последовательные выстрелы, очевидно, что заряды были идентичными.
Возможно ли предположить наличие скрытых дефектов в снаряде, радикально повлиявших на К? – нет, снаряд раскололся бы именно по месту таких дефектов, что сделало бы их явными после выстрела.
Остаются два предположения:
Снаряд Wheeler-Sterling был аномально плох, а снаряд Jonson был аномально хорош. Аномалии встречаются, но одновременное их сочетание уж слишком аномально, тем более лично я привык к мысли, что в то время снаряды Wheeler-Sterling считались отличными, потому указанное предположение считаю несерьезным.
Тогда остается угол стрельбы. Рассчитывать на то, что испытатели для одного из выстрелов забыли дописать «направление выстрела 21 градус» немного наивно, потому зададимся вопросом точности определения такого угла.
Некоторые вопросы по баллистике
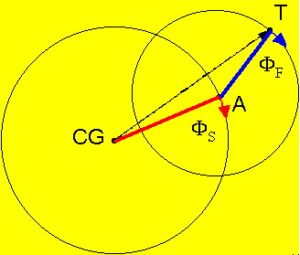
Вращательное движение снаряда представляет собой сумму трёх движений: нутации, прецессии и ротации. Устойчивость вращающегося снаряда обеспечивается за счет гироскопического эффекта. В случае с артиллерийским снарядом мы и имеем такую зависимость: опрокидывающий (дестабилизирующий) момент силы сопротивления воздуха вызывает прецессию снаряда и соответственно появление восстанавливающей пары, направленной противоположно опрокидывающему моменту. При достаточно большом числе оборотов снаряда вокруг оси величина восстанавливающего момента тоже велика, и при возмущающем воздействии внешних сил положение оси приблизительно сохраняется, давая лишь дополнительное движение оси вокруг первоначального положения – прецессию. Линия, около которой происходит это прецессионное движение, называется динамической осью.
Колебания и отклонения от главной прецессии называются нутацией. Если принять траекторию проходящей через точку CG, то носик снаряда в рамках прецессии должен описывать окружность, обозначенную буквой А, в рамках же нутации носик снаряда в рамках должен описывать окружность, обозначенную буквой Т:
Это значит, что есть некоторая траектория (линия, вдоль которой перемещается центр тяжести снаряда), также некоторый угол положения носика снаряда относительно такой траектории.
В результате движение носика снаряда может быть представлено в виде следующей схемы:
Очень упрощенно говоря, направление носика гироскопически стабилизированного снаряда в атмосфере может быть упрощенно описано как угол траектории + угол прецессии + угол нутации, где угол процессии и угол нутации могут иметь как положительное, так и отрицательное значение относительно угла траектории.
Соответственно движение гироскопически стабилизированного снаряда в атмосфере может быть схематически показано следующим рисунком, где красная линия показывает угол траектории, так как он определен в таблицах стрельбы и рассчитывается баллистическим калькулятором, а синяя линия показывает направления носика снаряда относительно угла траектории (рисунок из книги Никифоров Н.Н. «Артиллерия». Военное издательство Министерства обороны Союза СССР. М. – 1953).
Удовлетворительных способов хотя бы прикинуть, чему там были равны какие углы в ходе описанной коллегами стрельбы 09.05.1896 мне сыскать не удалось.
Немного современной эмпирики
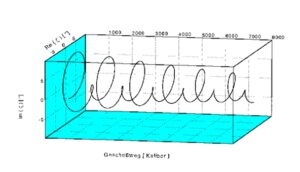
Мне не удалось найти оцифрованные результаты мгновенной фотофиксации начальной стадии полета современных снарядов на расстояния порядка 100 метров, потому рассмотрим таковые в отношении некоторых современных пуль, где по оси Х отображено расстояние в калибрах ствола, по осям Y и Z отображено рыскание пули. Если представить, что центр тяжести движется по прямой линии, расположенной в координатах Y = 0 и Z = 0, то кривая линия будет отображать положение носика пули. (Заранее прошу прощения за некоторую примитивность изложения в целях краткости).
Рыскание бронебойной пули патрона 7,62х51 стандарт НАТО:
Максимальный угол рыскания до 13 градусов (затухающий). Период рыскания между двумя экстремумами составляет примерно восемь метров, то есть, около 1 000 калибров.
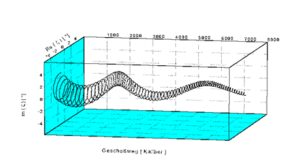
Рыскание бронебойной пули патрона 5,56х45 стандарт НАТО:
Максимальный угол рыскания до 6 градусов (затухающий). Период рыскания между двумя экстремумами составляет примерно семь метров, то есть, около 1 250 калибров.
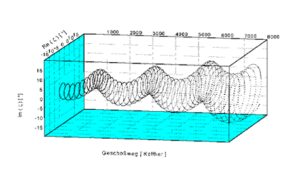
Рыскание пули патрона KTW 0.357 magnum
Максимальный угол рыскания до 3 градусов (затухающий).
Рыскание пули патрона Wadcutter 0.38 special
Угол рыскания на исследуемой дистанции от 5 до 15 градусов (возрастающий).
Правда будем честны и отметим, что обычный патрон 5,56х45 стандарт НАТО дает максимальный угол рыскания до 2 градусов (стабильный), а обычный патрон к 5,45х39 к АК-74 (так в оригинале) дает максимальный угол рыскания до 4 градусов (затухающий).
Важность этих данных заключается в том, что они собраны для дистанций, которые для крупнокалиберных орудий соответствуют дистанциям до 250-300 метров, то есть, именно тем дистанциям, на которых проводились опытовые стрельбы по определению пробития брони.
Краткие выводы:
1.Пули одного и того калибра, выпущенные из одного и того же ствола, могут иметь в разы отличающийся между собой по значению угол рыскания, который зависит от конструкции конкретного патрона.
2.Рыскание пули может иметь затухающий, стабильный или возрастающий характер.
3.Период между максимальными значениями (экстремумами) рыскания «правильно» стабилизированной пули составляет около 1 000 – 1 250 калибров.
4.Для затухающего характера рыскания максимальное значение достигается в первом периоде.
5.Несмотря на важность достижения малых значений рыскания для бронебойных пуль, все достижения современной баллистики позволили сократить значение угла рыскания (первый период рыскания) не более чем до 6 – 13 градусов.
Немного запоздалого троллинга
Предположим, что стрельба проводится бронебойной пулей патрона 7,62х51 стандарт НАТО, где максимальный угол рыскания до 13 градусов (затухающий), а период рыскания между двумя экстремумами составляет примерно восемь метров, то есть, около 1 000 калибров. Допустим, что с дистанции около 8 метров сделано 2 выстрела: первый под углом прицеливания Y = 0 градусов и Z = 0 градусов, а второй под углом прицеливания Y = 0 градусов и Z = 21 градус.
В первом случае предположим, что пуля двигалась с постоянным углом прецессии в 11 градусов от угла прицеливания и с углом нутации в 2 градуса от угла прецессии, тогда она попала в мишень под реальным углом встречи равным 0± от 9 до 13 градусов.
Во втором случае предположим, что пуля двигалась с постоянным углом прецессии в 11 градусов от угла траектории и с углом нутации в 2 градуса угла прецессии, тогда она попала в мишень под реальным углом встречи равным 21± от 9 до 13 градусов.
Но у нас нет проблемы с пулей, у нас есть проблема со снарядом.
Перенесем результаты пули на снаряд.
В первом случае предположим, что снаряд двигался с постоянным углом прецессии в 11 градусов от угла прицеливания и с углом нутации в 2 градуса от угла прецессии, тогда он попал в плиту под реальным углом встречи равным 0 ± от 9 до 13 градусов.
Во втором случае предположим, что снаряд двигался с постоянным углом прецессии в 11 градусов от угла прицеливания и с углом нутации в 2 градуса от угла прецессии, тогда он попал в плиту … ой, таки не смешите меня, чтоб снаряд уровня 1896 года не ушел на рикошет, да еще и осилил 15 дюймов брони при 21 плюс 13 градусов?! А 21 минус 13 градусов, будет 8 градусов.
При такой аналогии ужели мы можем предположить, что снаряд Юры из Хабаровска попал в плиту под углом не 0 градусов, как он принял в расчетах, а 13 градусов? – легко! При такой аналогии мы даже точно знаем, что он всяко не попал в плиту под углом менее 9 градусов.
При такой аналогии ужели мы можем допустить, что снаряд Андрея из Челябинска попал в плиту под углом не 21 градус, как он принял в расчетах, а 8 градусов? – а в чем собственно проблема?!
Поджигание стула вопросами нормализации снаряда в тему статьи не входит, потому …
Продолжаем думать
Если взятый по таблицам стрельбы или баллистическому калькулятору a = угол траектории, то угол встречи = a ± результирующий угол отклонений от угла траектории.
Немного преобразуем формулу
V = K*(d^0,75*b^0,7)/(G^0,5*cos a)
в формулу
V = K*(d^0,75*b^0,7)/(G^0,5*cos (a ± поправка на угол отклонений от угла траектории)).
Как было сказано выше, исходный коэффициент К получается по результатам подстановки в формулу результатов опытовой стрельбы («эмпирический выстрел») и применяется для расчета результатов последующих стрельб идентичным типом снарядов в идентичный тип брони.
Тогда для одного конкретного выстрела указанную формулу можно преобразовать в иной вид, учтя результирующий угол отклонений от угла траектории в К, формула примет вид:
V = (K номинальный + поправка` на результирующий угол отклонений от угла траектории) *(d^0,75*b^0,7)/(G^0,5*cos a)
или же:
V = (K истинный ± 38 попугаев) *(d^0,75*b^0,7)/(G^0,5*cos a)
где ± 38 попугаев означает некое неизвестное нам случайное количество попугаев в пределах от минус 38 попугаев до плюс 38 попугаев, а сами попугаи могут быть толстыми и тонкими, длинными и короткими.
Если же полученный по результатам одного выстрела К формата (K истинный ± 38 попугаев) применить к моделированию второго «теоретического» выстрела, то придется второй раз брать поправку и формула Жакоба де Марра при первом приближении упрощенно будет иметь вид:
V = ((K истинный ± 38 попугаев ± 38 ворон) * (d^0,75*b^0,7)/(G^0,5*cos a)
где ± 38 ворон означает некое неизвестное нам случайное количество в пределах от минус 38 ворон, до плюс 38 ворон, сами вороны могут быть толстыми и тонкими, длинными и короткими.
При этом нет никаких оснований утверждать, что эти «еще попугаи» должны быть равны первым попугаям количественно или качественно.
Еще раз смотрим рисунок из книги Никифорова Н.Н., как он есть, по осям Х и Y:
И грустно замечаем, что 38 ворон либо тянут снаряд носиком вниз, чем увеличивают потребный путь в вертикальной броне, либо тянут снаряд носиком вверх, чем создают неприятный разворачивающий момент, стремящийся опрокинуть снаряд на вертикальную броню плашмя.
Еще раз смотрим рисунок из книги Никифорова Н.Н., представляя, что ось Х осталась, а вместо оси Y у нас ось Z (вместо падения деривация):
И грустно замечаем, что 38 ворон тянут снаряд носиком то вправо, то влево, и ладно бы у нас была плоская плита, так назло вместо нее у нас круглый барбет «Сикисима», что еще более увеличит результирующий угол.
Еще немного современной эмпирики
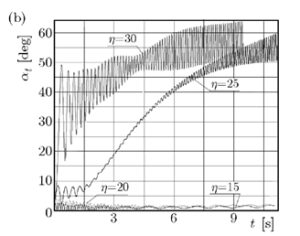
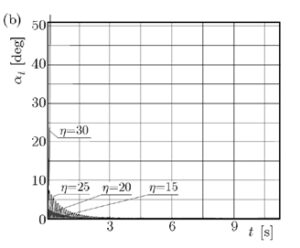
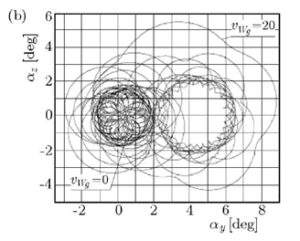
Рассмотрим графическое отображение поиска наивыгоднейшего решения баллистики для 155-мм снаряда с точки зрения классических для второй половины 20 века представлений:
Выше видим Аt – размер угла рыскания для разных решений при стрельбе с начальной скоростью 319 метров в секунду и углом прицеливания в 10 градусов.
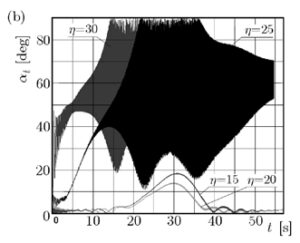
Выше видим Аt – размер угла рыскания для разных решений при стрельбе с начальной скоростью 935 метров в секунду и углом прицеливания в 10 градусов.
Выше видим Аt – размер угла рыскания для разных решений при стрельбе с начальной скоростью 319 метров в секунду и углом прицеливания в 70 градусов.
Выше видим Аt – размер угла рыскания для разных решений при стрельбе с начальной скоростью 935 метров в секунду и углом прицеливания в 70 градусов.
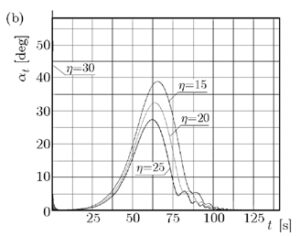
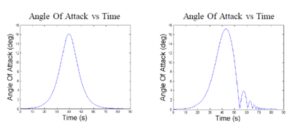
Ниже отобразим путь носика снаряда для наивыгоднейшего решения при стрельбе с начальной скоростью 935 метров в секунду и углом прицеливания в 10 градусов с точки зрения классических для второй половины 20 века представлений.
Ниже отобразим путь носика снаряда для наивыгоднейшего решения при стрельбе с начальной скоростью 935 метров в секунду и углом прицеливания в 10 градусов с учетом ветрового воздействия с точки зрения классических для второй половины 20 века представлений.
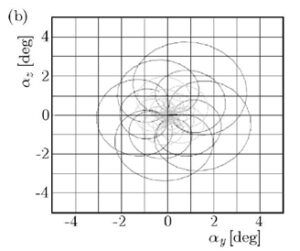
Сравним поведение носика одного и тоже снаряда на одном и том же участке траектории в реальной атмосфере по модели с 6 степенями свободы (слева) и в теоретической атмосфере по той же модели с 6 степенями свободы (справа):
Умели раньше моделировать реальную атмосферу? – сомневаюсь.
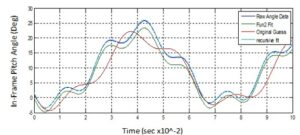
А также на указанном ниже примере сопоставим точность описания угла атаки одного и того же снаряда различными конкурирующими современными моделями на всей траектории полета:
Наконец, обратим внимание на современные данные о поведении 155-мм снаряда в первые 0,01 секунды полета:
Посмотрим на современную эмпирику в отношении снарядов, которая до сих пор опускает проблемы описания полета на сверхмалых дистанциях, и сделаем грустный вывод, что ранее детально моделировать движение снаряда просто не могли, потому игнорировали, что на дистанциях опытового обстрела броневых плит угол встречи снаряда с броней мог оказаться совершенно не таким, как это принято думать.
Ну, как игнорировали, если выстрелить раз десять при одинаковых условиях, то закономерность вывести можно, а вот один выстрел дает, скажем так, некоторую погрешность. Потому один выстрел у Юры из Хабаровска примерно такой же аргумент, как и один выстрел у Андрея из Челябинска.
А как было раньше с баллистикой
По-разному, например вот так:
«В 1 ч. 49 мин. пополудни, когда из японской эскадры успели лечь на новый курс только «Миказа» и «Сикисима» — два из двенадцати,— с расстояния 32 кабельтовых раздался первый выстрел «Суворова», а за ним загремела и вся эскадра… Я жадно смотрел в бинокль…
Некоторые из длинных японских снарядов на этой дистанции опрокидывались и, хорошо видимые простым глазом, вертясь, как палка, брошенная при игре в городки, летели через наши головы не с грозным ревом, как полагается снаряду, а с каким-то нелепым бормотанием.
-Это и есть «чемоданы» («Чемоданами» в Артуре называли японские длинные снаряды больших калибров. В самом деле: снаряд — фут в диаметре и более 4 футов длины, разве это не чемодан со взрывчатым веществом?)?- спросил, смеясь, Редкий.
Они самые… Однако меня тут же поразило, что «чемоданы», нелепо кувыркаясь в воздухе и падая как попало в воду, все-таки взрывались. Этого раньше не было…». (капитан 1 ранга Семенов В.И. «Бой при Цусиме»)
«12-дм снаряд, попавший в сухарное отделение и неразорвавшийся, был извлечен оттуда наверх мной. Снаряд оказался длиной около четырех футов, сталь очень мягкая, ведущий поясок широкий, сплошной, из желтой меди. Трубка очень строгая, боек имел выступающими 4,5 оборота биконного винта, на боек навинчивался груз, который препятствовал в обычное время жалу бойка коснуться капсюля. При вращении снаряда на полете груз свинчивался с бойка и освобождал жало. Многие из нас заметили, что на далеких дистанциях полет японских снарядов был неправильный, они кувыркались через голову. Стенки фугасного снаряда сравнительно очень тонкие, разрывной заряд помещался в двух шелковых мешочках, его было около 70-ти фунтов, и шимоза по наружному виду очень похожа на меленит, но только бледнее его и с запахом камфоры, вероятно ее примешивали». (капитан 2 ранга Лутонин С. И. «Деятельность броненосца “Полтава” в русско-японскую войну 1904 года»)
Ужели русские офицеры видели именно то, что они думали, что видят? Об этом как-нибудь в другой раз. Просто сделаем грустный вывод, что раньше с баллистикой могло быть очень не очень.
И что же Гончаров? Да, ничего, по сути, он написал, как знали в то время, — снаряд стабилен на основном протяжении полета, значит, влияние последствий гироскопического движения на сопротивление учтем внутри эмпирических зависимостей.
Вот только, если быть щепетильным, почти мгновенное торможение в стальную плиту и длинный путь в атмосфере – несколько различные процессы, а стабильность на основном протяжении полета – слабое утешение при оценке потенциальной ошибки результатов опытов по пробитию брони при стрельбе «в упор».
Как показано выше, «cos a» в формуле Жакоба де Марра не соответствует углу оси от носика снаряда к центру его донца, «cos a» в формуле Жакоба де Марра соответствует углу линии, по которой перемещается центр тяжести снаряда (траектории), что придает расчету по формуле Жакоба де Марра … несколько вероятностный характер.
Краткие промежуточные итоги
К де Марра определили с точностью ± случайное число в пределах до 38 неизвестного нам размера попугаев.
После этого экстраполировали полученные результаты на пробитие брони для другого снаряда из другой пушки по другой броне с точностью ± случайное число в пределах до 38 неизвестного нам размера ворон.
Что скажете?