Статья из жж Андрея Фирсова.
Текст Анатолия Сорокина
Перед тем, как перейти к теме «что делать при отсутствии таблиц стрельбы при грубой наводке орудия», окончательно закроем, как сейчас модно говорить, «гештальт» по предыдущей части IVб. В ней на практике измерялось, хотя и мысленно, смещение центра области разрывов по осям Х и Y в конкретной обстановке при изменении прицела и угломера на 1 тысячную. Стоит такой эксперимент целых 12 выстрелов. Четыре из них уходят на точное определение координат точки накола (путём вычисления их средних значений для исключения влияния рассеивания). Следующие четыре снаряда нужны на ту же процедуру, но с «довеском» «плюс малость к прицелу, угломер фиксирован» применительно к установкам стрельбы для точки накола. И ещё четыре потребуются на то же самое, но с установкой «прицел фиксирован, плюс малость к угломеру».
В реальной жизни такое не используется почти никогда, поскольку есть таблицы стрельбы и там указано, насколько изменяется дальность огня при изменении угла возвышения, а при известной дальности нет проблем рассчитать, как изменятся координаты центра области разрывов при изменении прицела и угломера. Тригонометрия тут нам в помощь. Рассмотрим такой пример, более реальный, чем в предыдущей «серии» (коллеге Денису Силаеву с «Альтхистори» спасибо за наводящий вопрос по теме, собственно из ответа ему автора этот пример и взят, только уточнён ряд численных величин).
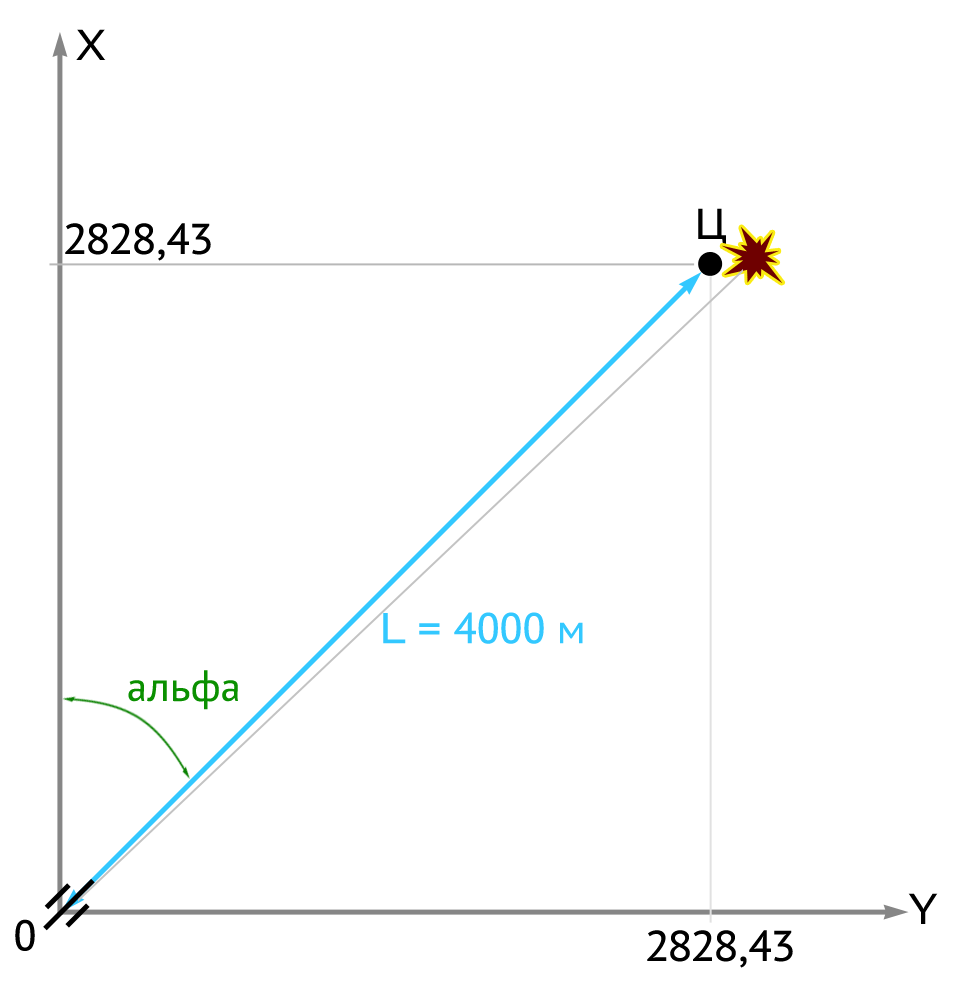
Цель – ДЗОТ противника, удалён от огневой позиции 152-мм гаубицы обр. 1938 г. (М-10) на 4000 м (топографическая дальность) точно на северо-восток. Т. е. дирекционный угол цели α, он же буссоль, равен 7-50 в делениях угломера (здесь «буссоль» – не сам угломерный прибор, а соответствующий направлению отсчёт на его шкале или шкалах). В более привычных единицах «альфа» равно 45 градусам или π/4 (0,785) радиан. Угол места цели равен нулю: ДЗОТ не выше и не ниже орудия, находится на его горизонте. Корректировку огня осуществляет самолёт-артиллерийский разведчик У-2. Заряд дан первый (хотя тут достаточно и наименее мощного восьмого, но пусть так), из таблиц стрельбы для этих условий сразу известно:
• Установка прицела A для дистанции L = 4000 м равна 129 по шкале тысячных для нормальных условий.
• Изменение прицела dА на 1 тысячную ведёт к изменению дальности огня dL на 23 м при любой разумной комбинации иных параметров стрельбы.
• Установку угломера B надо взять левее на 4 тысячных от используемого ориентира (не всегда головка панорамы смотрит по направлению стрельбы), так чтобы ствол был направлен по буссоли 7-46 для компенсации деривационного ухода снаряда вправо от линии огня.
Из этого, используя тригонометрию, сразу же получим (с учётом «артиллерийского» направления оси Х на север):
X = L×cos(α), dX = dL×cos(α), Y = L×sin(α), dY = dL×sin(α)
Соответственно, в численном выражении:
X = 4000×cos(7-50) = 2828,43 м, Y = 4000×sin(7-50) = 2828,43 м (координаты цели в системе координат с центром на огневой позиции орудия).
dX = 23×cos(7-50) = 16,26 м, dY = 23×sin(7-50) = 16,26 м.
А теперь вспомним формулы с частными производными из предыдущей «серии» и сразу же получим, что ∂Fx/∂A = +16,26 м/тыс. и ∂Fy/∂A= +16,26 м/тыс. в точке А = 129 при каком-то фиксированном B, соответствующему буссоли 7-50.
Столь же непринуждённо получим и остальную парочку ∂Fx/∂B и ∂Fy/∂B в точке с буссолью 7-50 при фиксированном А = 129. Для этого «подёргаем» немножно дирекционный угол: пусть его значение будет 7-51 (45 градусов 3,6 угл. минуты), т. е. dB = 1 при L = 4000 м. Те же косинусы и синусы посчитать труда не составит, результатом будет:
X = 4000×cos(7-51) = 2825,46 м, Y = 4000×sin(7-51) = 2831,39 м
Т. е. в наших условиях изменение дирекционного угла (буссоли) α на «малость» в 1 тысячную привело к уменьшению координаты Х на dX = 2,96 м и к увеличению координаты Y на dY = 2,96 м. То есть ∂Fx/∂B = -2,96 м/тыс. и ∂Fy/∂B = +2,96 м/тысячных. Можно, конечно, не так «дубово», а строго по науке продифференцировать синус и косинус по альфа и умножить оконечный результат на 0,001, но итог будет тот же самым.
Почему в расчётах фигурирует величина 7-50, а не 7-46 с учётом деривации? Потому, что нам нужно знать «чисто геометрический» вклад в боковое уклонение снаряда на направлении «орудие–цель», а его буссоль как раз 7-50. Да и разница между синусами/косинусами от 7-46 и 7-47, умноженными на 4000, равна по модулю 2,97 м (2,96 м для пары 7-50 и 7-51)– этим в расчётах можно смело пренебречь.
Все эти премудрости можно рассчитать ещё до стрельбы, зная дальность и направление на цель плюс основную зависимость дальности огня от угла возвышения ствола из таблиц стрельбы. Т. е. в нашем конкретном случае жуткая система уравнений
ΔX = ∂Fx/∂A×ΔA + ∂Fx/∂B×ΔB
ΔY = ∂Fy/∂A×ΔA + ∂Fy/∂B×ΔB
Превращается в куда менее страшную:
ΔX = 16,3×ΔA – 3,0×ΔB
ΔY = 16,3×ΔA + 3,0×ΔB
Даём первые четыре выстрела, не зная никаких параметров погоды, ничего об износе орудия, после чего ждём доклада лётчика-наблюдателя. Тот сообщает, что центр области разрывов лёг на 30 метров севернее и на 40 метров восточнее вражеского ДЗОТа. Явный перелёт с небольшим уклонением вправо, ветер снаряду дует попутный, да ещё и немного вбок его сносит. Учесть, увы, эту погодную прихоть нельзя – анемометра нет, по штату батарее времён Великой Отечественной войны (и даже тяжёлой гаубичной артиллерийской бригаде) не положен и в прошлом бюллетене «Метеоогневой» параметров ветра также нет: совсем недавно поднялся. Ждать же новый бюллетень от метеослужбы просто некогда. Ясно, что для компенсации влияния этого ветра прицел надо уменьшить, а ствол повернуть левее. Вопросы «насколько уменьшить и насколько левее» даёт решение оконечной системы уравнений с округлёнными значениями производных (ибо их значения с двумя знаками после запятой избыточны по точности, а вручную с меньшим количеством цифр считать легче):
30 = 16,3×ΔA – 3,0×ΔB
40 = 16,3×ΔA + 3,0×ΔB
Что должен тут узреть студент-первокурсник физматнаправленности? Нет, на сей раз не Огюстена-Луи Коши, а светлый лик «короля математиков» Карла-Фридриха Гаусса применительно к практическим задачам высшей алгебры. Да, линейная система уравнений второго порядка – школьная вещь без особых премудростей, но вот уже численное решение такой системы третьего порядка и выше без метода его имени никак не обойдётся.
Кстати, программирование алгоритма численного решения даже такой простой системы уравнений методом Гаусса – вовсе не тривиальная задача, Форсайт, Малькольм и Моулер не дадут соврать…
Итог: ΔA = 2,1 тыс., ΔB = 1,6 тыс. На эти величины нужно было бы увеличить прицел и угломер, чтобы попасть, куда попали (X = 2858 м, Y = 2868 м) при нормальных условиях (стандартная атмосфера без ветра, снаряд и заряд с табличными параметрами, новое орудие и т. п.). А для совмещения центра области попаданий с целью в реальных условиях (т. е. для компенсации их влияния на полёт снаряда) надо эту операцию проделать «в другую сторону». То есть вычесть ΔA из значения прицела и вычесть ΔB из значения угломера (с учётом алгебраического знака этих приращений, конечно). Округляем их и командуем расчёту уменьшить прицел на 2 тысячных (станет 127), а угломер взять левее на 2 тысячных (буссоль станет 7-44 с учётом деривации), после чего сразу же беглый огонь на разрушение цели! Центр области разрывов ляжет с хорошей точностью в точку с координатой Х около 2828 м и Y около 2828 м.
Все эти выкладки показывают нам, как можно использовать производные и их численные значения на практике, в данном случае для быстрого переноса огня в желаемое место. Рассчитать эти значения производных для воздушной корректировки огня по странам света можно по таблицам стрельбы, если известны координаты своих орудий и цели (см. пример выше). А если «двенадцатиснарядной» процедурой из части IVb определить их «по факту», то можно точно поражать врага, даже не зная, где находятся наши огневые позиции, видя только результат ведения огня в окрестности цели, что само по себе довольно круто. Возможно, что в каких-то нестандартных случаях такой подход окажется полезным (в стандартных ситуациях применяются проверенные долгой практикой стандартные же методы действий). Но на то артиллеристу и голова дана, чтобы, зная природу вещей, успешно решать боевые задачи во всяких условиях, которые даже не прописаны в уставах, поучениях, наставлениях и прочих методических пособиях. Русская/советская/российская артиллерия такими кадрами всё время славилась.
Под занавес этого дополнения: математика и впрямь творит чудеса, превращая 12 выстрелов в возможность точной корректировки огня, не зная даже местонахождения своих орудий, имелась бы только односторонняя связь с их расчётами. Гарри Потный и прочие чудотворцы отдыхают! Но и это ещё не всё – та же математика способна «порешать» боевую задачу вообще без таблиц стрельбы, только имея информацию о свойствах важных в артиллерийском деле функций. Но об этом в следующий раз.
PS. Предыдущая запись: О таблицах стрельбы, часть IVб (снова таблицы стрельбы большей частью отсутствуют)
источник: https://afirsov.livejournal.com/942182.html