Геометрия камеры Царя пирамиды Хеопса и равенство значений площади и периметра ряда двумерных фигур, объема и площади – трехмерных
На основании анализа геометрии помещения «Камера Царя» пирамиды Хуфу интерпретированы расстояния вписанного в геометрию этого помещения прямоугольного треугольника (рисунок 1). На рисунке показаны два прямоугольных треугольника вписанных в геометрию параллелепипеда (помещение – «Камера Царя»), где 2,618… – квадрат значения «золотого сечения» (1,618… 2), меньшее из ребер (AD) = 2*2,618… (5,236.. м), высота фигуры (DB) = √5*2,618… (5,854… м). При этом, прямоугольный треугольник А, D, С имеет уникальные свойства (в этом отношении рассматриваемый треугольник уникален), когда цифровое значение его площади 27,416… совпадает с таковыми значениями периметра и квадрата меньшего катета (рисунок 1).
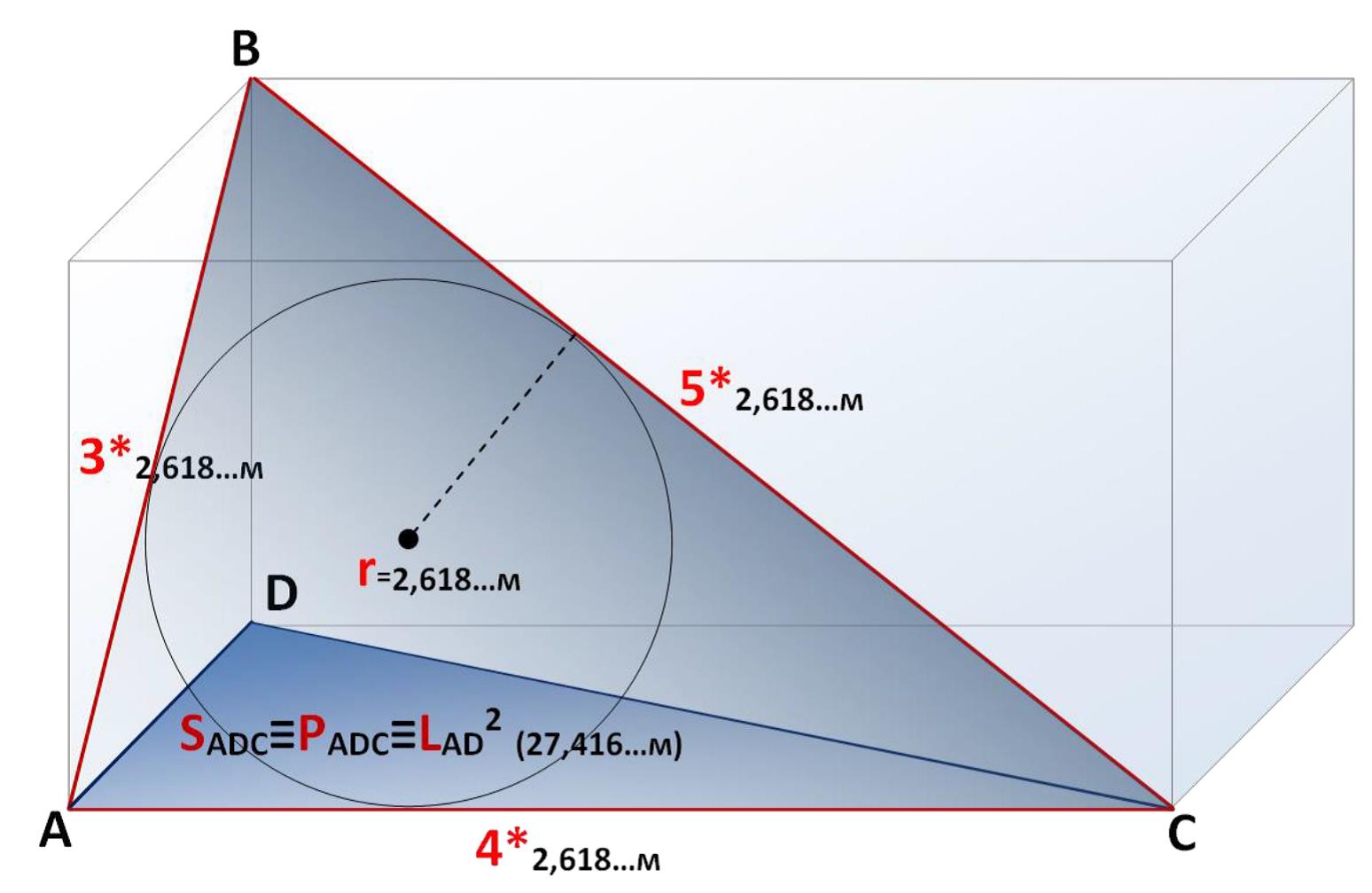
Рисунок 1 – Схематичное изображение геометрии помещения пирамиды Хеопса – «Камера Царя», где: 2,618… – квадрат значения «золотого сечения» (1,618… 2), меньшее из ребер (AD) = 2*2,618… (5,236.. м), высота фигуры (DB) = √5*2,618… (5,854… м)
В связи с результатами анализа геометрии помещения «Камера Царя» пирамиды Хуфу поставлена задача поиска возможных вариантов геометрических фигур, в которых наблюдаются равенства значений площади и периметра для двумерных фигур, объема и площади – для трехмерных.
По результатам расчетов выявлены следующие числовые равенства площади и периметра ряда двумерных фигур:
– квадрата, когда сторона равна 4 (площадь и длина периметра, соответственно, будут равны значению 16), радиус вписанного круга равен 2, а описанного — значению √8, диагональ квадрата равна √32;
– круга, когда наблюдается равенство площади и длины окружности при значении 12,566… или 4 π (радиус вписанного круга равен 2);
– прямоугольных треугольников с иррациональным значением площади и периметра, когда площадь и длина периметра первого равна значению 27,416324… ≡(√5+3)2 (где меньший катет — 5,236… будет равен √27,416324…, а больший — удвоенному значению меньшего — 10,472 …) и второго, когда катеты равны 6,8285… ≡(√2+2)*2 — при значении площади и периметра 23,314… ≡(√8+2)2. Радиус вписанного в треугольник круга равен 2;
– героновых треугольников со сторонами: (5, 12, 13 и 6, 8, 10 – прямоугольные треугольники), когда площадь и периметр первого равен значению 30, а второго — 24; 6, 25, 29; 7, 15, 20; 9, 10, 17 … (тупоугольные треугольники с площадью и периметром равные соответственно 60, 42, 36), радиус вписанного в названные треугольники круга равен 2;
– равностороннего прямоугольного треугольника, при значении площади 20,7846… или =√3*12 (при этом длина стороны равна 6,928…≡√48 или =√3*4), радиус вписанного круга равен 2 (рисунок 2).

Рисунок 2 — Наглядное представление различных четырех возможных прямоугольных треугольников удовлетворяющих равенству S=P
По результатам расчетов выявлены следующие числовые равенства объема и площади ряда трехмерных фигур:
– куба при грани равной значению √8, объем и площадь поверхности куба – 216, радиус вписанной сферы равен 3 (рисунок 3);
– сферы (равенство объема и площади поверхности) равной значению 113,097335526… или 36 π (при этом диаметр сферы равен 6, а ее окружность – 18,85…≡6 π), радиус вписанной сферы равен 3;
– тетраэдра (равенство площади и объема) равной значению 374,123… (при этом длина ребра равна 14,69693845669907…≡√216), радиус вписанной сферы равен 3 (рисунок 3);
– октаэдра (равенство площади и объема) равной значению 187,061… (при этом длина ребра равна 7,348469228349534…≡√54), радиус вписанной сферы равен 3 (рисунок 3);
– икосаэдра (равенство площади и объема) равной значению 136,4595… (при этом длина ребра равна 3,9695…), радиус вписанной сферы равен 3 (рисунок 3);
– додекаэдра (равенство площади и объема) равной значению 149,8578… (при этом длина ребра равна 2,694168…), радиус вписанной сферы равен 3;

Рисунок 3 – Платоновы тела (без додекаэдра) имеющие линейные размеры на основании размера вписанной в них сферы радиусом в 3 условных единицы
– цилиндра (равенство площади и объема) равной значению 54π ≈ 169,646… (при этом радиус равен 3, а высота – удвоенному значению радиуса – 6). Площадь боковой поверхности равна 113,097… (объем и площадь вписанной в фигуру сферы) или 36π, а площадь одного из двух оснований – 9π, радиус вписанной сферы равен 3. Объем цилиндра больше объема вписанной в него сферы (где есть равенство значений площади и объема) ровно в 1,5 раза;
– конуса (равенство площади и объема) равной значению 96π ≈ 301,593… (при этом радиус основания равен 6, образующая – 10, а высота – фигуры – 8). Площадь основания (круга) равна 113,097… (объем и площадь вписанной в фигуру сферы) или 36π, площадь боковой поверхности, соответственно, – 60π, радиус вписанной сферы равен 3;
– трехгранной пирамиды (равенство площади и объема тетраэдра) при высоте 12, стороне основания – 14,6969384567…≡√216 и равно значению 374,123…, радиус вписанной сферы равен 3;
– четырехгранной пирамиды (равенство площади и объема) при высоте 12, стороне основания – 8,485281374…≡√72 и равно 288. Отношение высоты к стороне основания – √2. При этом площадь боковой поверхности пирамиды в три раза больше площади основания (216 и 72), радиус вписанной сферы равен 3;
– шестигранной пирамиды при высоте 12, стороне основания – 4,898979485…≡√24 и равно 249.415…, радиус вписанной сферы равен 3.
На основании проведенных расчетов сформулировано заключение:
в двумерных фигурах: квадрат, круг, прямоугольный, тупоугольный и равносторонний треугольники радиус вписанной окружности при равенстве значений площади и периметра равен 2;
в трехмерных фигурах тетраэдр, куб, октаэдр, икосаэдр, додекаэдр, конус, цилиндр, 3-4-6-гранная пирамида и сфера радиус вписанной окружности при равенстве значений площади и объема равен 3.






