Статья из жж Андрея Фирсова.
Текст Анатолия Сорокина
Готовиться к этому заранее, конечно! Например, можно на разных углах возвышения «в поле» отстрелять орудие, даже незнакомое, и по факту тем самым составить те самые таблицы стрельбы, если есть время, место и прорва снарядов. Но речь сейчас не о том, а о ситуации, когда главная часть таблиц стрельбы – зависимость дальности стрельбы L от угла возвышения α для конкретного снаряда и заряда всё же известна, но вот с собой её нет ни в каком виде. Т. е. управляющему огнём недоступны ни система АСУНО с такими данными, ни книга или брошюра (классический вид таблиц стрельбы), ни нарезка дистанционных шкал на прицеле орудия. Последнее встречалось в истории нашей артиллерии не раз и не два, например, на прицелах 152-мм гаубиц-пушек обр. 1937 г. и 122-мм пушек обр. 1931/37 гг. (А-19) дистанционные шкалы штатно отсутствовали, имелась только шкала тысячных (т. е. угла возвышения). В 1940–42 гг. некоторые 122-мм гаубицы обр. 1938 г. (М-30) и 152-мм гаубицы обр. 1938 г. (М-10) также комплектовались прицелами без дистанционных шкал.

Дистанционный барабан прицела 122-мм гаубицы обр. 1938 г. (М-30) со всеми положенными шкалами. Экспозиция Военно-исторического музея артиллерии, инженерных войск и войск связи (ВИМАИВиВС) в г. Санкт-Петербурге

Дистанционный барабан прицела 122-мм гаубицы обр. 1938 г. (М-30) только со шкалой тысячных, экспозиция ВИМАИВиВС
Можно ли с приемлемой точностью свести весь изложенный в таблицах стрельбы массив данных L(α) для конкретного снаряда и заряда, скажем к трём легко запоминаемым цифрам, из которых его можно получить, не используя никаких таблиц, а из счётных машин – только инженерный калькулятор (наше время) или логарифмическую линейку (для времён Великой Отечественной)? Если знаешь и любишь математику, то легко!
Для начала вспомним таковые для зависимости L(α). Для начала «заумь mode on!»
Движение снаряда в вертикальной плоскости, где L – горизонтальная координата в направлении стрельбы, а H – высота его подъёма над плоскостью горизонта орудия, подчиняется таким уравнениям:
m×d²L/dt² = –Fгориз (dL/dt)
m×d²H/dt² = –m×g – Fверт(dH/dt)
где m – масса снаряда, t – время, g – ускорение свободного падения, а Fгориз и Fверт – горизонтальная и вертикальная проекции аэродинамической силы сопротивления движению, зависящей в первую очередь от соответствующей проекции текущей скорости снаряда (dL/dt и dH/dt на языке производных). Ну а d²L/dt² и d²H/dt² будут горизонтальной и вертикальной проекциями ускорения снаряда, всё по II закону Ньютона.
Вместе с начальными условиями в момент t = 0: L = 0, H = 0, dL/dt = V₀×cos(α), dH/dt = V₀×sin(α) всё это даёт задачу Коши (где V0 – модуль начальной скорости), которая при определённых условиях решается аналитически. Её решение даёт нам некий момент T, когда координата H вновь станет равной нулю (снаряд подброшен вверх, сила тяжести его заставила вернуться вниз и упасть на землю). Значение функции L(T) будет дальностью полёта для некоего угла возвышения α, варьируя это «альфа», можно получить и важную для артиллеристов зависимость от него величины L.
Самое простое решение, известное со школы – сферический конь cтрельба в вакууме, когда сила сопротивления среды F отсутствует в принципе. Выкладки здесь приводить не буду, но их результат, автор надеется, всё же не забыт: L(α) = D×sin(2×α), где D – максимальная дальность стрельбы, достигаемая при угле возвышения 45 градусов или π/4 радиан или 750 наших тысячных или 800 натовских mil’ов. Вот если сила сопротивления F нулю не равна, то всё становится гораздо интереснее. Часто её принимают за какую-то степень от скорости тела в воздушной среде. Кстати, в этом случае уравнения выше решаются аналитически, раздел «диффуры» в помощь, но попытки автора получить хоть какое-то соответствие с таблицами стрельбы окончились наиэпичнейшим провалом. И понятно почему: на «сверхзвуке» сопротивление движению снаряда подчиняется одним правилам, на дозвуковой скорости – уже другим, так что про «аналитику» тут лучше забыть. Только приближённое численное решение и всё тут! Иначе бы сначала дамочки за партами с логарифмическими линейками не понадобились бы для такой работы, которых потом злобные капиталисты из экономии взяли и заменили бездушным ENIAC’ом и ему подобным «железом». Да и мы не отстали в этом плане – в т. ч. и для нужд артиллерийских вычислений в 1947 году ввели в эксплуатацтю первый советский цифровой компьютер МЭСМ. Тем самым плавно «заумь mode off!»
Но это не повод отступаться от поставленной в начале статьи цели. L(α) уже не «Дэ на синус от двух альфа», но нечто сохраняющее важнейшие свойства этой функции на интервале значений α от 0 до 45 градусов (750 тыс.):
1) Функция L(α) непрерывная и гладкая (дифференцируема вообще бесконечное число раз), т. е. её график не имеет скачков, «улётов в бесконечность», «углов» и острых мест, вроде тех, что порождает модуль или ему подобные операции;
2) Она монотонно возрастает от нуля при аргументе ноль, но это возрастание становится всё медленнее и медленнее по мере подхода α к 45 градусам, а после эта функция и вовсе начинает убывать, так что в точке α = 45 градусов имеет место её максимум (как и в вакуумном «конносферическом» случае).
А давайте эту функцию заменим чем-нибудь легкосчитабельным, без «диффуров» и даже таблиц (синус сразу же в пролёте), вдруг четырёх арифметических действий (сложение, вычитание, умножение, деление) окажется вполне достаточно, чтобы получить приемлемое приближение? ОК, где Сорокин, там и 152-мм гаубица обр. 1938 г. (М-10), с максимальной дальнобойностью в 13290 м (по таблицам стрельбы, условия нормальные), вот для неё измыслим такое приближение (только α выразим в наших артиллерийских тысячных):
L(α) = 13290×(1 – (α – 750)² / 750²)
Это кусок сдвинутой и опрокинутой вниз рогами параболы, если кто ещё школу помнит. Удовлетворяет ли такое приближение озвученным выше критериям? Однозначно: L(0) = 0, L(750) = 13290 и максимально в этой точке на интервале от 0 до 1500 тыс., непрерывность, гладкость и монотонное возрастание при аргументе от 0 до 750 тыс. – всё выполнено. Теперь главное: а в точность хотя бы плюс минус 300 метров от значений настоящих таблиц стрельбы попадает? А нисколечки:
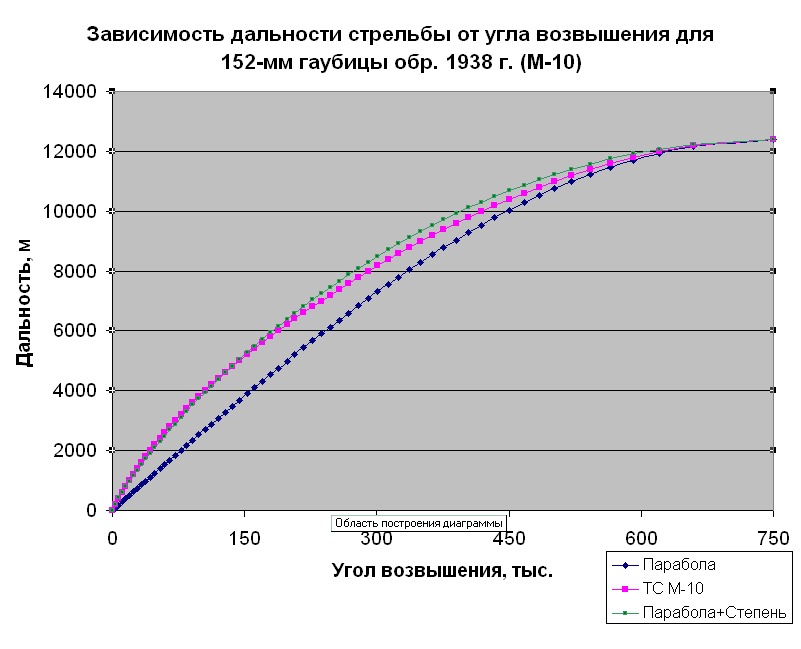
Тёмно-синяя кривая – параболическое приближение, фиолетовая – данные из таблиц стрельбы гаубицы М-10. Но впору процитировать Зайца из 15-й серии «Ну, погоди!»: «Но я не унываю, я сам себя спасаю, ничто на этом свете не сбудется само!» Вспоминаем, что математика – это наука о превращениях, и нам надо превратить тёмно-синюю кривую на графике в нечто подобное фиолетовой, сохранив при этом её прохождение через точки α = 0, L = 0 и α = 750, L = 13290. Какое заклинание (Гарри Потный снова в пролёте, как стая напильников) надо использовать из всего того, что только доступно со времён Пифагора до наших дней? Попробуем возведение в степень, в нашем случае 0,75, подтянем график вверх по оси ординат:
L(α) = 13290×(1 – (α – 750)² / 750²)⁰·⁷⁵
Результатом будет зелёная кривая на графике. Цель, в принципе, достигнута – разница между таким приближением и данными из таблиц стрельбы не превышает 300 метров, да и то только в диапазоне значений α от 200 до 600 тысячных, а вблизи опорных точек 0 и 750 совпадение просто отличное. Всё равно без блока поправок на атмосферные условия и состояние системы придётся пристреливаться, а там ошибка в 300 метров вполне терпима. Воздушный или наземный наблюдатель первый разрыв в точке накола не пропустит (в реальности и с таблицами стрельбы не раз случалось, что его засечь не удавалось, но то были ошибки топогеодезической привязки ведущего огонь орудия или цели, или ошибка в вычислениях, что считаем в нашем случае исключённым). Т. е. вместо обширного блока данных нам достаточно запомнить цифры 13290 (ну должен же артиллерист знать предельную табличную дальность своей матчасти назубок), алгоритм приближения «парабола рогами вниз» (с входящим в него параметром 750 тыс., но он неизменен для любых ситуаций) и степень 0,75. С этими легко запоминаемыми данными на бумаге всегда можно (пусть и за какое-то счётное время) получить приемлемое для практики приближение к реальной зависимости L(α).
Самое поганое во всей этой схеме – использование степени. Её на бумаге так просто не посчитаешь, нужен инженерный калькулятор или логарифмическая линейка (вспоминаем свойства логарифма: логарифм произведения равен сумме логарифмов множителей, логарифм от числа в некоей степени равен произведению этой степени на логарифм числа). Посему с логарифмической линейкой всё в итоге сводится к сложению и вычитанию, что высоко ценилось вычислителями всех времён и народов, в т. ч. и советскими артиллерийскими.

Логарифмические линейки активно использовались в артиллерии Красной Армии, а позже и в Советской до прихода цифровых ЭВМ
Заметим, что никакие бумажные таблицы (хоть стрельбы, хоть значений синуса, хоть логарифмов) в процессе не используются, только то, что заложено в легко доступные для своего времени вычислительные устройства под рукой. Но применялось ли такое в годы Великой Отечественной войны? Скорее всего нет, т. к. проще было хотя бы по основным точкам зависимости L(α) скопировать на бумаге её числовые величины или вообще нарисовать их краской на задней стороне щита орудия (немцы для своих le.FH.18 давали легко копируемую номограмму на миллиметровке для такой ситуации и наши специалисты отмечали удобство её использования, но почему-то не внедрили подобный подход у себя). Сейчас с развитием систем АСУНО и коммуникаций (интернет есть и на поле боя) можно легко получить необходимые данные. Так значит всё вышеизложенное – только гимнастика ума без приложения к практике? А вот и нет!
Был период в развитии электронной цифровой вычислительной техники, когда памяти было немного, но элементарные алгебраические операции и основные функции уже считались очень быстро (в отличие от прямого решения дифференциальных уравнений, описывающих движения снаряда в воздушной среде). Это программируемые инженерные калькуляторы и первые карманные ЭВМ вроде «Электроника МК85».

Первый компьютер автора, приобретённый в 1992 году. Для старшеклассника и студента тех лет – просто улёт, сколько времени он сэкономил при расчётах на «лабах» в универе (с прошедшим Днём студента, кстати!). 16-битный чисто отечественный процессор с системой команд PDP-11 (олдскульные программеры тут начинают вспоминать «великие были времена, великая была техника…»), 32 Кслов (64 Кбайт) адресуемой памяти, из которых 5317 байт было доступно пользователю для программ и данных (в модификации «М», а без неё – вовсе 1221 байт). Бейсик в качестве языка программирования (весьма неплохой, кстати) с возможностью попиксельного вывода на 12-знакоместном экране (одно знакоместо 5х7 пикселов) и даже созданием спрайтов (можно закодировать свой символ в знакогенераторе). Всё ещё работает, если удаётся запустить (со временем стало барахлить ПЗУ, из за чего может функционировать сразу после первого включения, а может и после двадцатого)
Их активно внедряли в практику артиллерийских вычислителей и автор встречал не раз упоминания при личном общении и в интернете о том, как это устройство реально позволяло в разы убыстрить расчёты установок для стрельбы, если заранее заложить в него программы решения типовых задач. В отличие от КШМ вроде 1В13, 1В14 (где громоздкие большие цифровые ЭВМ полагались штатно) такой компьютер можно было взять с собой, а армейские умельцы-радиолюбители вполне себе быстро доукомплектовывали его полевым источником питания 6 вольт (на батарейках он долго не тянул). И, естественно, кое-кто из армейских изобретателей и рационализаторов хотел использовать в подобных устройствах в т. ч. данные из таблиц стрельбы: ввёл координаты цели, орудия и сразу установки прицела и угломера получить на выходе без гроссбухов вроде многотомника «Таблицы стрельбы 152-мм гаубицы обр. 1943 г. (Д-1) для равнинных и горных условий»: потаскай-ка его с собой! Памяти для хранения всей информации оттуда не хватало, но алгоритм приближённого и быстрого расчёта нужных величин можно было в «Электронику МК85» вложить нехилый, получше вышеизложенного, с куда более высокой точностью, чем 300 м. Затем была ещё более крутая «Электроника МК95», а потом нашим изделиям такого рода пришёл белый пушной северный зверёк Alopex lagopus. Когда же появились импортные наладонники и планшеты, то там уже можно было держать сканы бумажных таблиц стрельбы или создать программу, где они заложены целиком как есть, а потому и надобность в приближённых методах их расчёта отпала. А уж когда состоялось пришествие АСУНО, где чуть ли не «диффуры» в реальном времени считаются, то и приспособление гражданской техники к военным нуждам отправилось туда же, в архив истории прикладного вычтеха.
Но даже такой кратковременный эпизод раскрывает нам всю мощь и возможности математики. Её знание это круто и с ним не пропадёшь. Так что всем первокурсникам совет: посмотреть на портрет Огюстена-Луи Коши, прочесть открывающее портал в глубины анализа заклинание «для любого строго положительного эпсилон найдётся такое натуральное эн большое, зависящее от эпсилон, что при любом эн малом, большем, чем это эн большое … (и т. д. по определению предела)» и в конце концов освоенной на пятёрку магией производных и интегралов сразить противника в лице профессора или доцента на экзамене! После этого драйв на кураже обеспечен … до следующего экзамена или сессии, так что удачи.