Многогранник Дюрера и составная трехмерная модель симметричного геометрического объекта

Аннотация. Исследованы два варианта геометрии многогранника Дюрера – условно названные как «традиционный» и «альтернативный». Выявлены геометрические свойства обеих вариантов многогранников. По результатам натурного эксперимента выявлено, что «альтернативный» вариант многогранника обладает свойством комплементарности.

Ключевые слова: многогранник Дюрера, симметричный объект, трехмерная модель, геометрический объект.

Введение. Многогранник Дюрера – многогранник, изображённый на гравюре Альбрехта Дюрера «Меланхолия §I» (рисунок 1). Массивный многогранник расположен у основания лестницы и доминирует в левой половине гравюры. Точная геометрия этого тела сегодня является предметом незаконченных научных споров.

Рисунок 1 – Гравюра Альбрехта Дюрера «Меланхолия §I» (1514 г.)

Основная часть. Нами исследованы два варианта геометрии многогранника Дюрера. Один (условно названный нами «традиционный» [5]) – с геометрическими параметрами шести больших граней: длина большей стороны грани соотносится к меньшей в отношении квадрата золотой пропорции (1), а средняя к меньшей – в отношении золотой пропорции (2). Большая и меньшая стороны рассматриваемой фигуры образуют между собой угол в 108°, а большие стороны – в 72° (рисунок 2, слева). Кроме того, установлены так же следующие равенства для «традиционного» многогранника Дюрера ((3), (4)). Предлагаемый нами многогранник – «альтернативный» – имеет геометрию больших шести граней, которую характеризуют равенства (5) и (6). Он может быть построен из четырех треугольников Фибоначчи – когда два больших треугольника соединены между собой большими катетами, а два других – меньших – прилегают своими гипотенузами к меньшим катетам больших треугольников Фибоначчи (рисунок 2, справа). (Треугольник Фибоначчи – прямоугольный треугольник с соотношением катетов равным золотой пропорции [1, 2, 3, 4]). Большая и меньшая стороны грани «альтернативного» многогранника образуют между собой угол ≈63,435…°Таким образом, получена геометрическая фигура, обладающая следующими свойствами (5), (6).

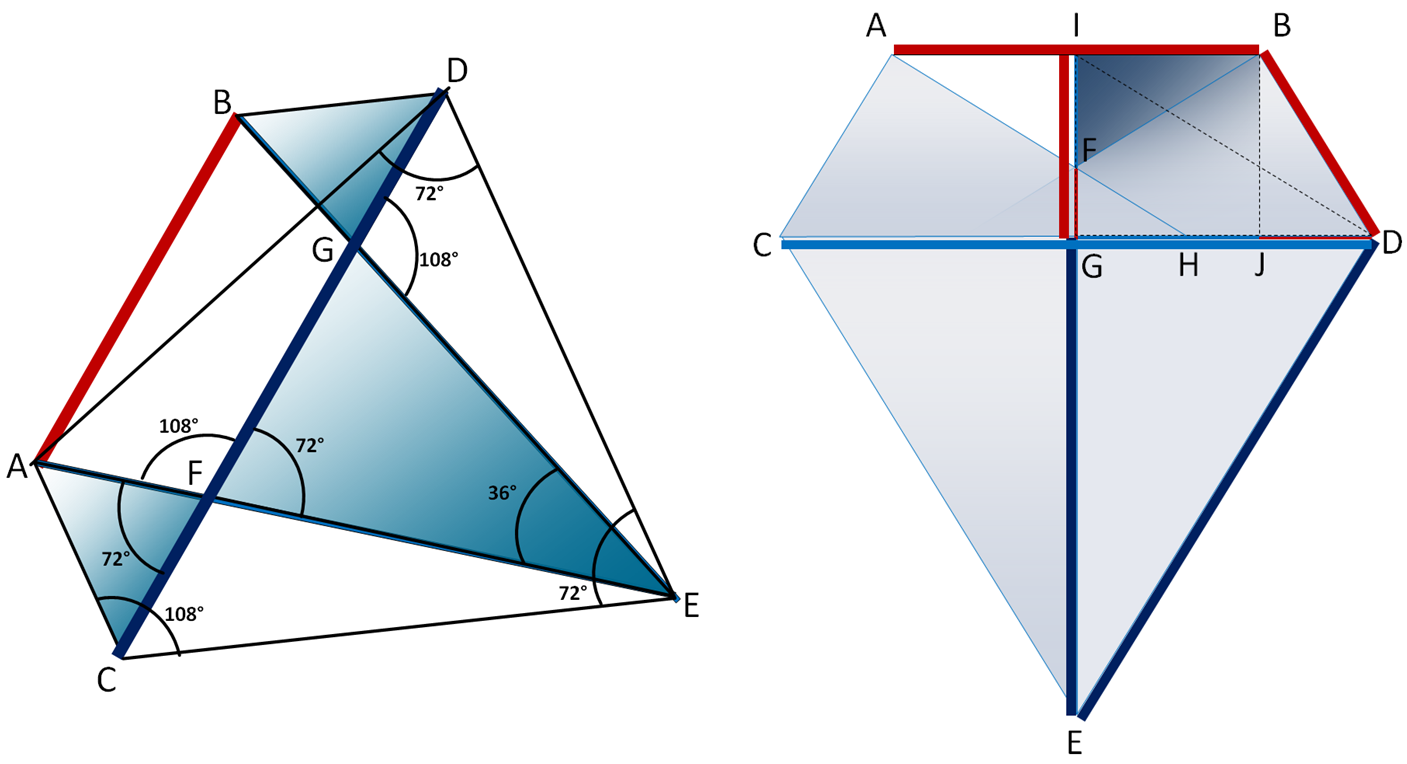
Рисунок 2 – Грань многогранника Дюрера. Два варианта представления грани многогранника: слева – традиционное, справа – альтернативное

FD/CF=FE/AF=АD/AC=1,61803…2                                                              (1)

FG/CF=CD/АB=1,61803…                                                                               (2)

АD=CE=DE                                                                                                          (3)

CD=AE=BE                                                                                                          (4)

CD/AB=AH/CA=IF/FG=FH/FG=EG/GD=GJ/JD=BJ/JD=1,61803…  (5)

ED/DB=EG/GI=1,61803…2                                                                              (6)

Для изготовления трехмерных моделей двух вариантов представления многогранника Дюрера были рассчитаны и расчерчены две развертки (рисунок 3). На их основе были изготовлены трехмерные натурные модели двух многогранников Дюрера (рисунок 4).

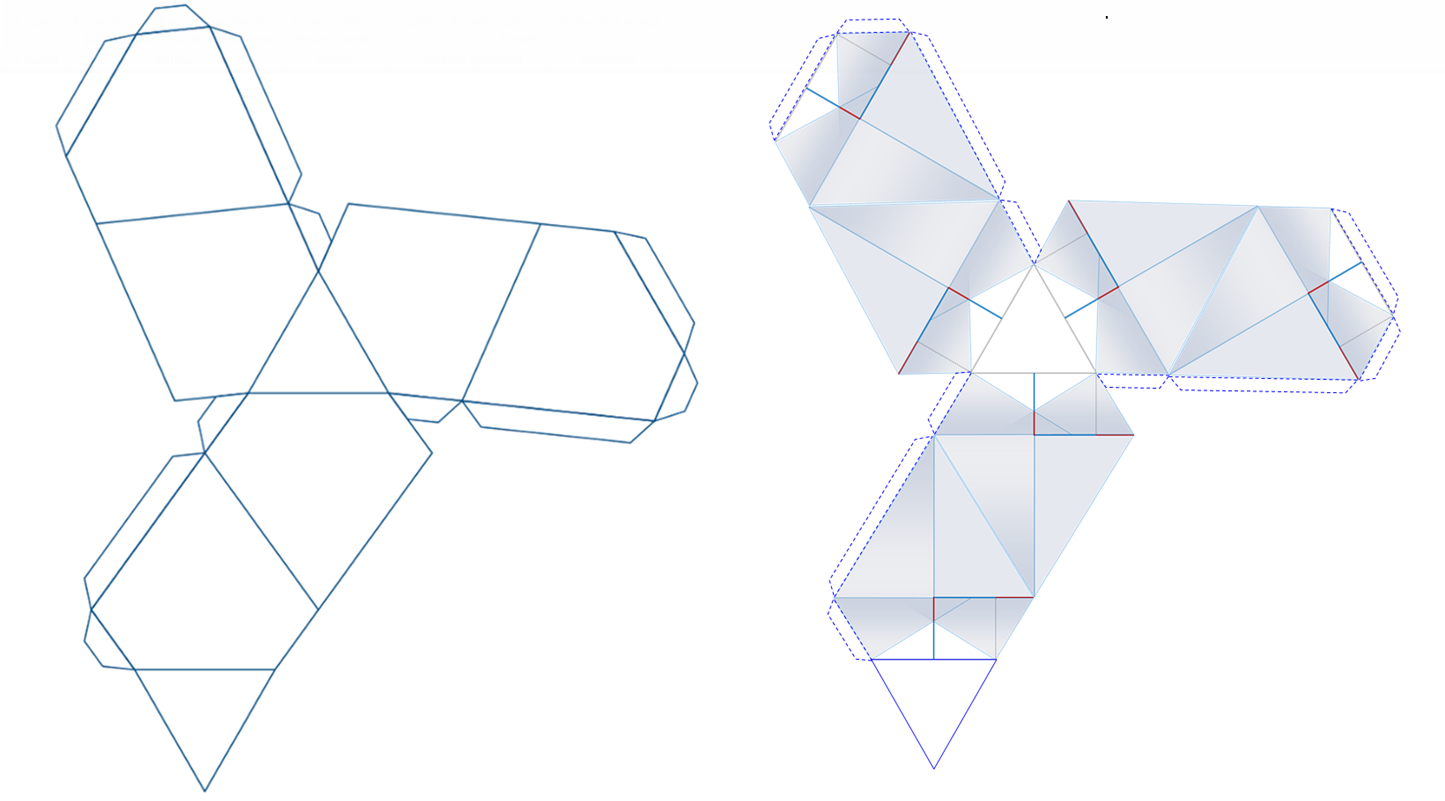
Рисунок 3 – Развертка «традиционного» (слева) и «альтернативного» (справа) варианта представления многогранника Дюрера

Рисунок 4 – Трехмерная модель двух вариантов представления многогранника Дюрера: слева – «традиционный», справа – «альтернативный» (фотография)

По результатам натурного эксперимента выявлено, что «альтернативный» вариант представления многогранника Дюрера обладает свойством комплементарности – многогранники образуют разнообразные составные геометрические объекты (как не симметричные, так и симметричные (рисунок 5, 6, 7, 8). Внутреннее пространство – полость – одной из составных моделей, образованное треугольными гранями двадцати «альтернативных» многогранников, имеет форму икосаэдра (рисунок 8).

Рисунок 5 – Трехмерная модель объекта составленного из девяти многогранников Дюрера (фотография)

Рисунок 6 – Трехмерная модель объекта составленного из двадцати многогранников Дюрера. Вид сбоку (фотография)

Рисунок 7 – Трехмерная модель объекта составленного из двадцати многогранников Дюрера. Вид сбоку-сверху (фотография)

Рисунок 8 – Трехмерная модель объекта составленного из десяти многогранников Дюрера (фотография)

Заключение.

1. Исследованы два варианта геометрии многогранника Дюрера – условно названные как «традиционный» и «альтернативный».
2. Выявлены геометрические свойства обеих вариантов многогранников.
3. По результатам натурного эксперимента выявлено, что «альтернативный» вариант многогранника обладает свойством комплементарности.

Список литературы:

1. Ворон, А.В. Геометрический треугольник Фибоначчи и пирамида Хеопса // «Академия Тринитаризма», М., Эл № 77-6567, публ.23546, 13.07.2017.
2. Ворон, А.В. Дуальность и комплементарность треугольников Кеплера, Фибоначчи и их связь с геометрией платоновых тел // «Академия Тринитаризма», М., Эл № 77-6567, публ.24401, 06.04.2018.
3. Ворон, А.В. Культорологический и технологический аспект великой пирамиды // «Академия Тринитаризма», М., Эл № 77-6567, публ.24005, 29.11.2017.
4. Ворон, А.В. Свойства треугольников Кеплера, Фибоначчи и их связь с геометрией пирамиды Хуфу // «Академия Тринитаризма», М., Эл № 77-6567, публ.24320, 04.03.2018.
5. https://www.jacquier.org/Art_contemporain/Yvo_Jacquier-Construction_Polyedre_Durer-3.pdf