«Структура» треугольника Кеплера, треугольника Фибоначчи и построение на их основе геометрии пирамиды Хуфу, платоновых тел

Аннотация. Показана возможность построения «структуры» треугольников Кеплера и (условно названного) треугольника Фибоначчи посредством трех отрезков, длина которых отражает математическую прогрессию золотого сечения. Показан способ получения чисел рекуррентного ряда Фибоначчи при посредстве треугольника Фибоначчи. На основе геометрии треугольников Кеплера и Фибоначчи создана математическая модель геометрии пирамиды Хуфу. Указанные треугольники Кеплера и Фибоначчи позволяют «строить» платоновы тела в соответствии с содержанием текста диалога Платона «Тимей».

Ключевые слова: треугольник Кеплера, треугольник Фибоначчи, геометрия пирамиды Хуфу, платоновы тела, золотая пропорция.

Введение. Известно классическое определение золотой пропорции как деление отрезка, в котором отношение большей части к меньшей равно отношению всего отрезка – к большей части (рисунок 1). Важно отметить в этой связи взаимосвязь трех размерностей. На это же обстоятельство указывает С.А. Алферов, поясняет [1]: «в последовательности отрезков «a-b-c» средним по длине отрезком является «b». Отсюда понятен смысл одного из старинных определений золотого сечения, как деления отрезка «на средний и крайний» (а не на два: больший и меньший), то есть – получение взаимосвязи 3-х». На это, без преувеличения, важное уточнение сегодня необоснованно мало обращают внимания.

Рисунок 1 – Деление отрезка в среднем и крайнем отношении, где: красный = 1; синий = 1,618…; зеленый = 2,618…

Основная часть. Известно отношение в треугольнике Кеплера между гипотенузой и меньшим катетом в виде золотой пропорции. К этому следует добавить еще и соответствующее отношение меньшего катета к меньшему отрезку гипотенузы ограниченного проекцией высоты треугольника Кеплера. Таким способом получена «структура» отражающая взаимосвязь трех отрезков в треугольнике Кеплера в виде своеобразной композиции формирующей этот прямоугольный треугольник (рисунок 2, слева). Следуя изложенной выше логике построения треугольника Кеплера, методом последовательного перебора вариантов построения композиций из трех обозначенных отрезков (рисунок 1) найдена другая «структура» (условно названного) треугольника «Фибоначчи» (рисунок 2, справа). Попытки смоделировать иные возможные композиции «структуры» прямоугольных треугольников из трех величин отрезков (рисунок 1) не принесли положительных результатов.

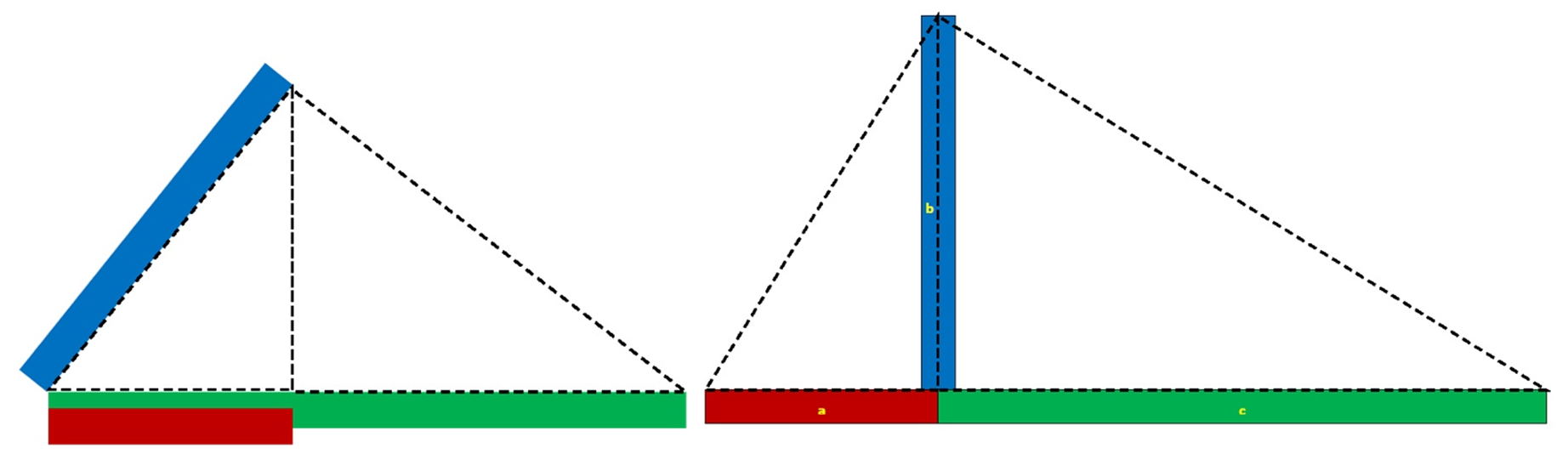
Рисунок 2 – Взаимосвязь трех отрезков отражающих понятие золотого сечения в треугольнике Кеплера (слева) и Фибоначчи (справа), где: красный = 1; синий = 1,618…; зеленый = 2,618…

Найденный таким образом треугольник «Фибоначчи» позволяет получить определенным образом числа рекуррентного ряда Фибоначчи. Если принять за величину размерности катетов треугольника «Фибоначчи» последовательные числа Фибоначчи, то квадрат гипотенузы будет равен соответствующей сумме их квадратов в виде числа Фибоначчи (рисунок 3). Например: 13²+8²=233; 8²+5²=89; 5²+3²=34; 3²+2²=13 и так далее.

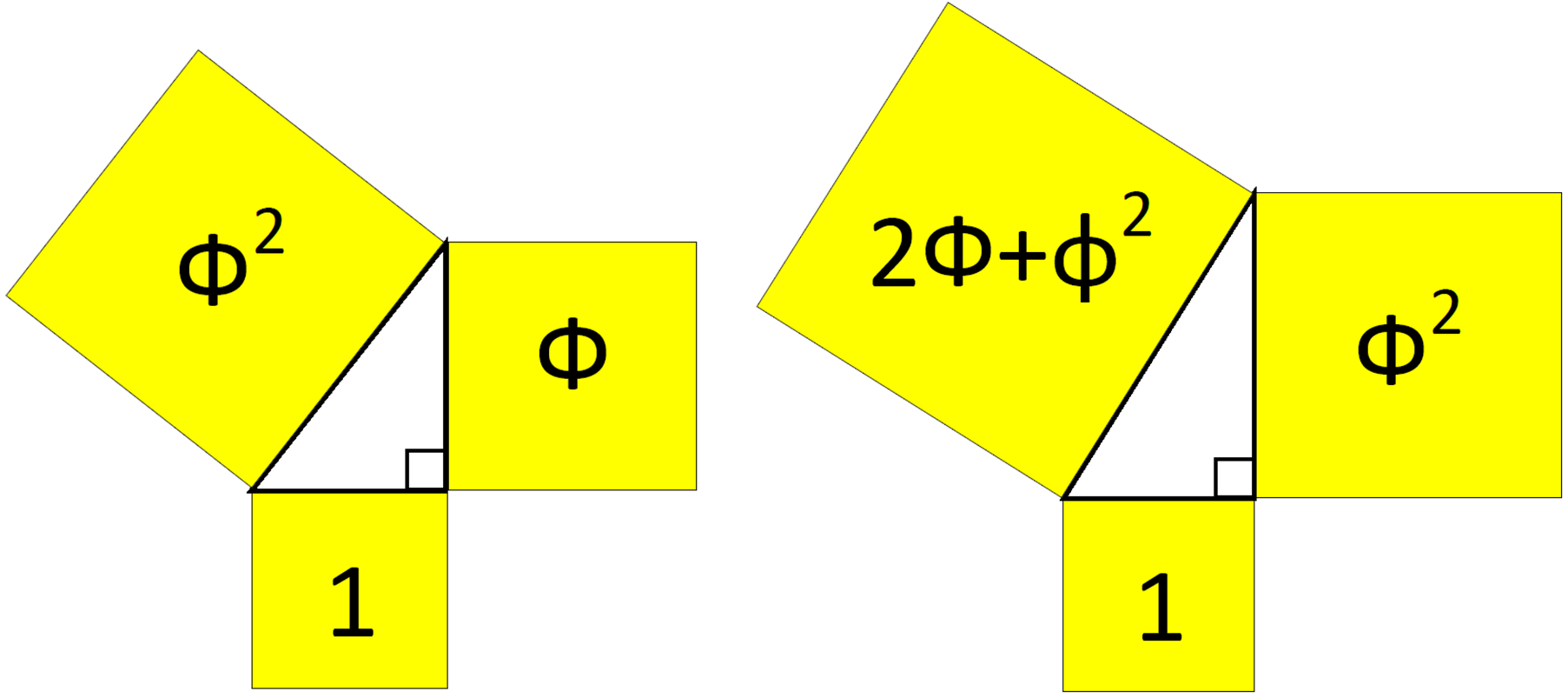
Рисунок 3 – Прямоугольные треугольники с квадратами катетов и гипотенуз: треугольник Кеплера (слева), треугольник Фибоначчи (справа), где: «Ф» и «ф» – соотношение «золотого сечения» (Ф=1,618… и ф=0,618…)

На основе геометрии треугольников Кеплера и Фибоначчи создана математическая модель геометрии пирамиды Хуфу [2, 3, 4] которая совпала (за исключением вогнутостей боковых поверхностей фигуры) с фактической геометрией сооружения (рисунок 4). В этой связи сформулировано предположение: при проектировании пирамиды Хуфу архитектор ориентировался, прежде всего, на геометрию двух треугольников – Кеплера и Фибоначчи [4].

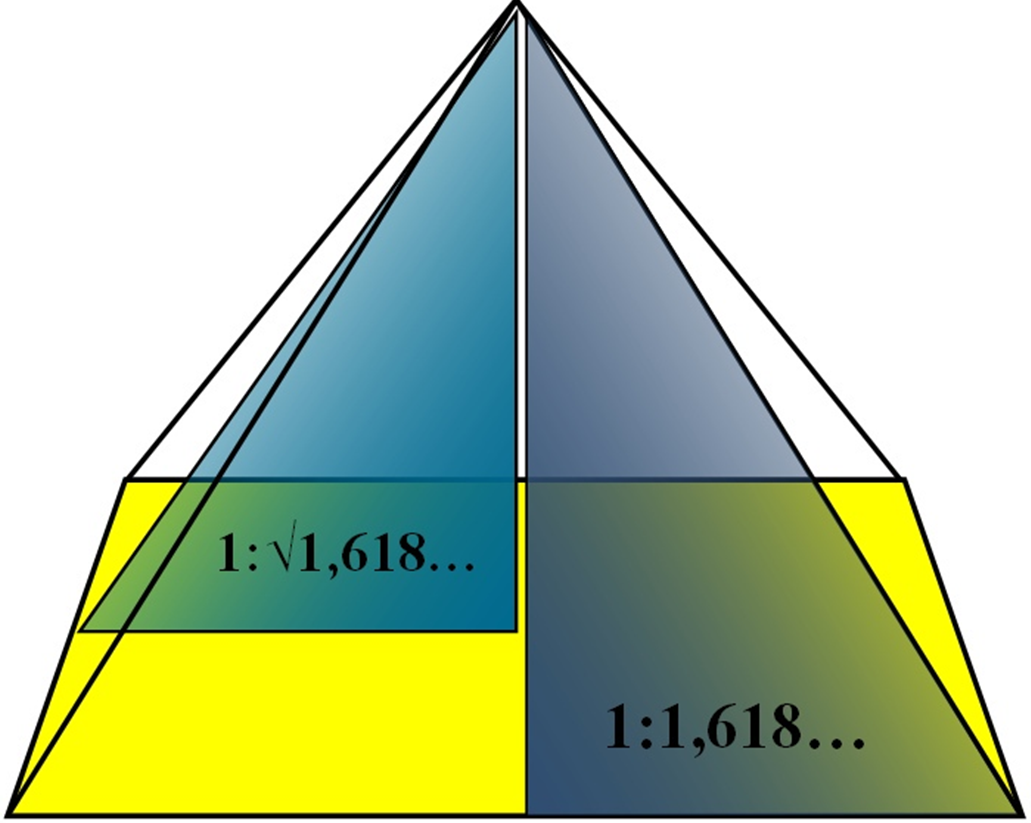
Рисунок 4 – Схематичное изображение геометрии пирамиды Хуфу посредством двух треугольников: Кеплера (слева) и Фибоначчи (справа) с указанием соотношений их катетов, где: √1,618… и 1,618… – корень значения и значение «золотого сечения»

Математическом способом была показана возможность построения платоновых тел из структурных элементов – треугольников Кеплера и Фибоначчи – при условии неизменности площади названных элементов [5] (рисунок 5). Количество элементов составляющих «структуру» «тетраэдра», «октаэдра», «куба» увеличивается, таким образом, в два раза, а «икосаэдра» – в пять раз по отношению к количеству элементов тетраэдра при неизменности показателя «площадь всех структурных элементов фигуры» (S_{c.э.1пл.т.}=√38 373) и радиуса (r=3) вписанной в платоновы тела сферы [5]. При этом расчет показал, что площадь структурных элементов двух додекаэдров (S_{c.э.2дод.}=√959 325) равна площади структурных элементов любых 5-ти платоновых тел, например, 5-ти тетраэдров, октаэдров, кубов, икосаэдров (S_{c.э.1пл.т.}=√38 373). Показанная возможность находится в соответствии с текстом произведения Платона «Тимей», согласно которому платоновы тела могут «перерождаться друг в друга… » [6].

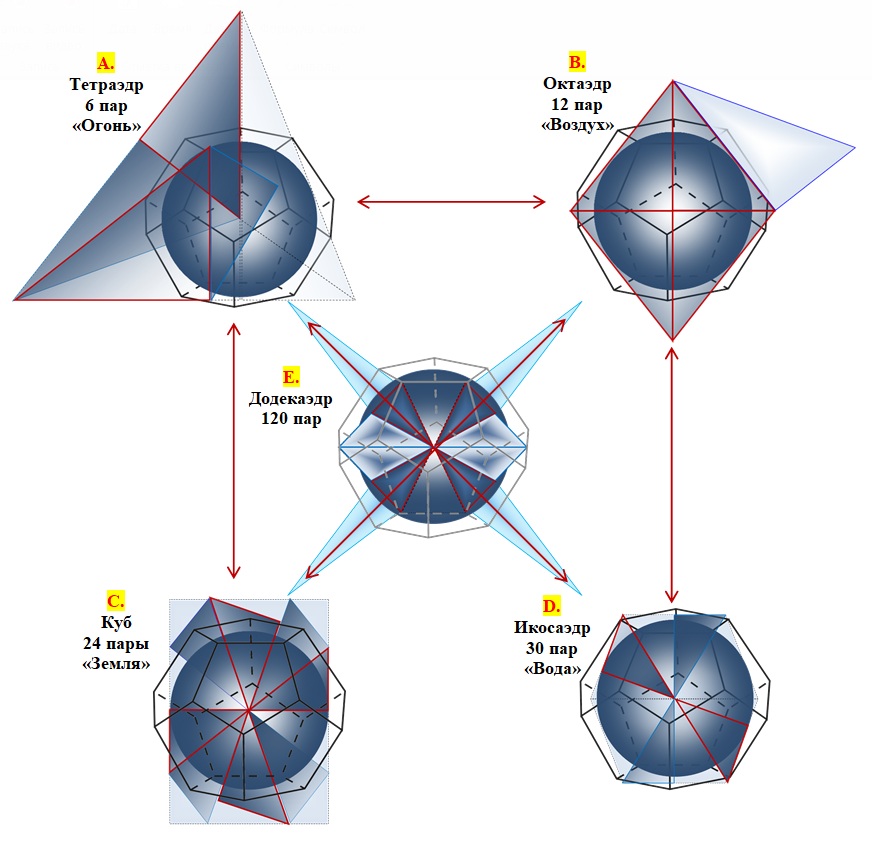
Рисунок 5 – Появление и взаимный «переход» платоновых тел и их количественные составляющие – пары элементов (треугольники Кеплера и Фибоначчи)

В связи с результатами теоретического исследования [5] сделано предположение: в диалоге Платона «Тимей» [6] под словами «Восприемница» и «Кормилица» подразумевалась мировая среда или «додекаэдрово поле» (рисунок 6), состоящее из элементов – множества додекаэдров, а под платоновыми телами «тетраэдр», «октаэдр», «куб», «икосаэдр» – фундаментальные частицы (в современной физике элементарных частиц – субатомная частица, которая не состоит из других частиц), которые, таким образом, могут обладать свойствами взаимного перехода (перерождения) и движения в (мировой) среде или в додекаэдровом поле.

Рисунок 6 – Модель «додекаэдрового поля» – два ракурса – из 13-ти элементов-додекаэдров «додекаэдрового поля» (фотографии)

Заключение.

1. Показана возможность построения «структуры» треугольников Кеплера и (условно названного) треугольника Фибоначчи посредством трех отрезков, длина которых отражает математическую прогрессию золотого сечения.
2. Показан способ получения чисел рекуррентного ряда Фибоначчи при посредстве треугольника Фибоначчи.
3. На основе геометрии треугольников Кеплера и Фибоначчи создана математическая модель геометрии пирамиды Хуфу.
4. Указанные треугольники Кеплера и Фибоначчи позволяют «строить» платоновы тела в соответствии с содержанием диалога Платона «Тимей».

Список литературы:

1. Алферов, С. А. Золотая пропорция, треугольник Паскаля и принцип квадр // «Академия Тринитаризма», М., Эл № 77-6567, публ.12706, 13.12.2005.
2. Ворон, А.В. Геометрический треугольник Фибоначчи и пирамида Хеопса // «Академия Тринитаризма», М., Эл № 77-6567, публ.23546, 13.07.2017.
3. Ворон, А.В. Культорологический и технологический аспект великой пирамиды // «Академия Тринитаризма», М., Эл № 77-6567, публ.24005, 29.11.2017.
4. Ворон, А.В. Свойства треугольников Кеплера, Фибоначчи и их связь с геометрией пирамиды Хуфу // «Академия Тринитаризма», М., Эл № 77-6567, публ.24320, 04.03.2018.
5. Ворон, А.В. Платоновы тела как структурированные геометрические объекты // «Академия Тринитаризма», М., Эл № 77-6567, публ.26288, 08.04.2020.
6. Платон. Тимей / Собр. соч. в 4-х т. Т 3. – М.: Мысль, 1994. – 654 с.